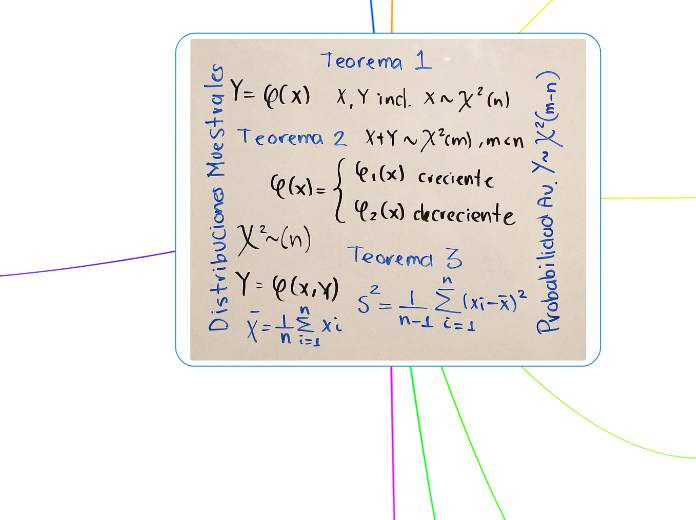
Teorema de Cambio de Variable 1

Def. Sea X una variable aleatoria continua con valores dentro de un intervalo (a,b) ∈ ℝ , y con función de densidad f(x).
Sea φ: (a,b) →ℝ, una función continua, estrictamente creciente o decreciente y con inversa diferenciable. Entonces la variable aleatoria Y= φ(x), tiene la siguiente función de densidad con su dominio.

Teorema de Cambio de Variable 2

Def. Sea X una variable aleatoria continua con valores dentro de un intervalo (a,b)∈ ℝ y con función de densidad f(x), entonces, si tenemos una φ(x) que sea creciente y decreciente para diferentes intervalos, se denotarán como φ1(x), φ2(x), respectivamente, cumpliendo que sean continuas, creciente y decreciente, y tengan inversas diferenciables, la función de densidad para la variable Y= φ(x) está dada por.

Tercer Teorema de Cambio de Variable

Def. Sea (X,Y) un vector continuo con valores en I⊆ℝ^2 y con función de densidad f(x,y). Sea φ(x,y): I→ℝ^2 una función continua con inversa φ^-1(u,v) diferenciable.
Entonces el vector (U,V)=φ(x,y) toma valores en φ(I) y tiene función de densidad.

Paso 1: Identificar la f(x,y) y su dominio.

Paso 2: Plantear el vector de transformación.

Paso 3: Hallar las inversas respectivas.

Paso 4: Utilizando el Teorema, elaboramos la f(u,v).

Paso 5: Hallamos el dominio de f(u,v).

Paso 6: Hallamos la función de densidad que nos pide.

Suma

x+y

Resta

x-y

y-x

xy

Cociente

𝑥/𝑦

𝑦/𝑥

Una muestra aleatoria son variables aleatorias x1, x2, ..., xn que cumplen el ser independientes e idénticamente distribuidas.

Un estadístico es cualquier función de la muestra, se dice que g(x1, x2, ..., xn) es un estadístico

X barra

𝑠^2

Media Muestral

Varianza Muestral