GEOMETRÍA ANALÍTICA, LINEAS RECTAS Y CIRCUNFERENCIAS
CONICAS
CIRCUNFERENCIA
se puede definir como la figura generada por una curva cerrada o perímetro en el cual no hay vértice ni ángulos internos.La circunferencia es una línea curva, cerrada y plana, cuyos puntos están todos a la misma distancia de otro punto, llamado centro.
CENTRO:punto central que está a la misma distancia de todos los puntos pertenecientes a la circunferencia
RADIO:pedazo de recta que une el centro con cualquier punto perteneciente a la circunferencia
CUERDA:pedazo de recta que une dos puntos cualquiera de una circunferencia
DIÁMETRO:mayor cuerda que une dos puntos de una circunferencia. Hay infinitos diámetros y todos pasan por el centro de la circunferencia
RECTA SECANTE:recta que corta dos puntos cualesquiera de una circunferencia
RECTA TANGENTE:recta que toca a la circunferencia en un solo punto y es perpendicular a un radio
ECUACIÓN CANONICA

EJEMPLO
PARÁBOLA
se define como el lugar geométrico de los puntos del plano que equidistan de un punto denominado foco, y una recta denominada directriz.El eje de la parábola es la recta perpendicular a la directriz, que pasa por el foco F. La distancia FD, del foco a la directriz, se denomina parámetro de la parábola, el punto medio del segmento FD, es el punto V, que se denomina vértice de la parábola.
FOCO:Es el punto fijo F
DIRECTRIZ:Es la recta fija D
PARÁMETRO:A la distancia entre el foco y la directriz de una parábola se le llama parámetro p
EJE:La recta perpendicular a la directriz y que pasa por el foco recibe el nombre de eje. Es el eje de simetría de la parábola
VÉRTICE:Es el punto medio entre el foco y la directriz. También se puede ver como el punto de intersección del eje con la parábola
RADIO VECTOR:Es el segmento que une un punto cualquiera de la parábola con el foco
ECUACIÓN CANÓNICA
EJEMPLO
ELIPSE
Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante
FOCOS:Son los puntos fijos F y F'
EJE FOCAL:Es la recta que pasa por los focos
EJE SECUNDARIO:Es la mediatriz del segmento FF'
CENTRO:Es el punto de intersección de los ejes
RADIOS VECTORES:Son los segmentos que van desde un punto de la elipse a los focos: PF y PF'
DISTANCIA FOCAL:Es el segmento segmento de longitud 2c, c es el valor de la semidistancia focal
VÉRTICES : Son los puntos de intersección de la elipse con los ejes: A, A', B y B'
EJE MAYOR:Es el segmento segmento de longitud 2a, a es el valor del semieje mayor
EJE MENOR:Es el segmento segmento de longitud 2b, b es el valor del semieje menor
EJE DE SIMETRÍA: Son las rectas que contienen al eje mayor o al eje menor
CENTRO DE SIMETRÍA:Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría
ECUACIÓN CANÓNICA
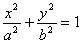
EJEMMPLO
HIPERBOLA
Es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos llamados focos es constante
FOCOS:Son los puntos fijos F y F'
EJE PRINCIPAL O REAL:Es la recta que pasa por los focos
EJE SECUNDARIO O IMAGINARIO:Es la mediatriz del segmento FF'
CENTRO:Es el punto de intersección de los ejes
VÉRTICES:Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal.Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c
RADIOS VECTORES:Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'
DISTANCIA FOCAL: Es el segmento de longitud 2c
EJE MAYOR:Es el segmento de longitud 2a
EJE DE SIMETRÍA:Son las rectas que contienen al eje real o al eje imaginario
ASINOTAS:Son las rectas de ecuaciones:

RELACIONES ENTRE LOS SEMIEJES:

ECUACIÓN CANÓNICA
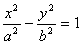
EJEMPLO
