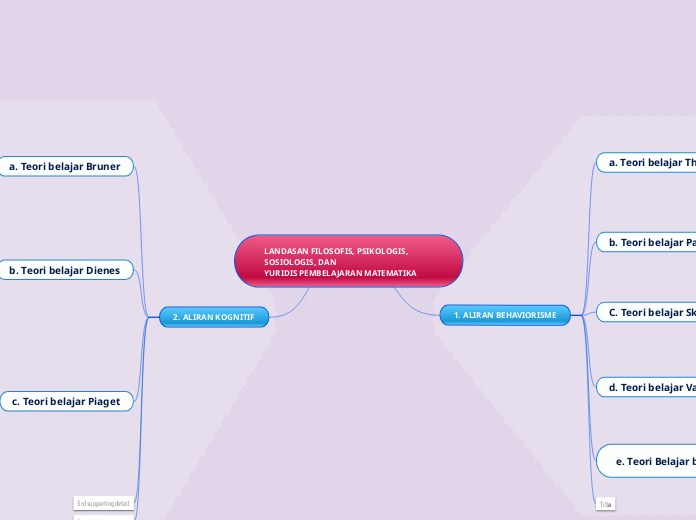
LANDASAN FILOSOFIS, PSIKOLOGIS, SOSIOLOGIS, DAN
YURIDIS PEMBELAJARAN MATEMATIKA
ALIRAN BEHAVIORISME
a. Teori belajar Thorndike
KARATERISTIK INTI MATEMATIKA:
menurut Susanto (2012) adalah:
(1) memiliki objek kajian abstrak,
(2) bertumpu pada kesepakatan (3) berpola pikir deduktif (4) memiliki simbol yang kosong
(5) memperhatikan semesta pembicaraan (6) konsisten dalam sistemnya.
KARATERISTIK INTI MATEMATIKA:
b. Teori belajar Pavlov
KARATERISTIK INTI MATEMATIKA: (1) Menggunakan rangsangan tertentu (2) Perilaku seseorang berubah sesuai dengan keinginan (3) Dapat menggunakan binatang sebagai eksperimen
C. Teori belajar Skinner
Teori Skinner menyatakan penguatan terdiri atas penguatan positif dan penguatan negatif. Penguatan dapat dianggap sebagai stimulus positif, jika penguatan tersebut seiring dengan meningkatnya perilaku siswa dalam melakukan pengulangan perilakunya
d. Teori belajar Van Hiele
Van Hiele (dalam Ismail, 1998) menyatakan bahwa terdapat 5 tahappemahaman geometri, yaitu:
1. Tahap Pengenalan 2. Tahap Analisis 3. Tahap Pengurutan 4. Tahap Deduksi 5. Tahap Keakuratan
2nd supporting detail
Bandura menyatakan bahwa proses belajar terjadi dengan mengalami dan meniru apa yang ada disekitarnya
ALIRAN KOGNITIF
a. Teori belajar Bruner
KARAKTERISTIK INTI MATEMATIKA: (1) Tahap-tahap dalam proses belajar - Tahap Enaktif - Tahap Ikonik - Tahap Simbolik (2) Teorema cara belajar dan mengajar matematika. - Teorema penyusunan (Construction theorem) - Teorema notasi (Notation theorem) - Teorema kekontrasan dan keanekaragaman (Contras and variation theorem) - Teorema pengaitan (Connectifity theorem) - Belajar Penemuan
b. Teori belajar Dienes
KARAKTERISTIK INTI MATEMATIKA: 1. Tahap Bermain Bebas 2. Tahap Permainan 3. Tahap Penelaahan Kesamaan Sifat 4. Tahap Representasi 5. Tahap Simbolisasi 6. Tahap Formalisasi
c. Teori belajar Piaget
KARAKTERISTIK INTI MATEMATIKA: (1) menunjukkan konsep Matematika yang dipelajari, menjelaskan keterkaitan konsep, mengaplikasikan
konsep atau algoritma, secara luwes, akurat, efisien dan tepat dalam pemecahan masalah (2) memiliki kemampuan mengkomunikasikan gagasan dengan simbol,tabel, grafik atau diagram untuk memperjelas keadaan atau masalah (3)menggunakan penalaran pada pola, sifat atau melakukan manipulasi Matematika dalam membuat generalisasi, menyusun bukti, atau menjelaskan gagasan dan pernyataan Matematika (4) menunjukkan kemampuan strategik dalam merumuskan, menafsirkan dan menyelesaikan model Matematika dalam pemecahan masalah dan (5) memiliki sikap menghargai kegunaan
Matematika dalam kehidupan.
3rd supporting detail
Concluding sentence