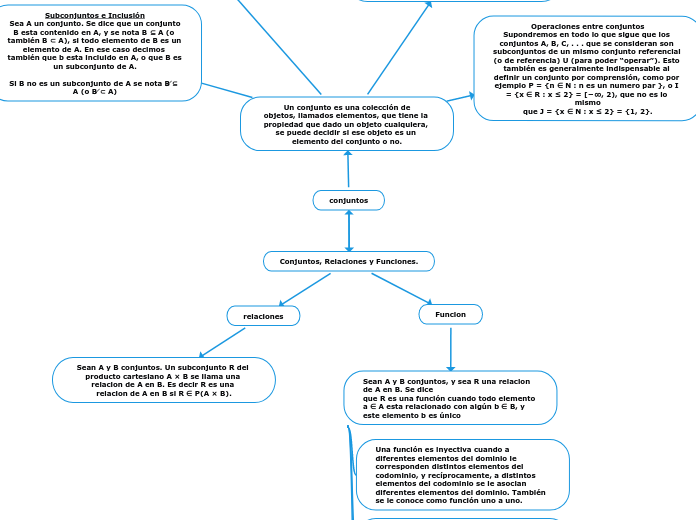
Conjuntos, Relaciones y Funciones.
conjuntos
Un conjunto es una colección de
objetos, llamados elementos, que tiene la propiedad que dado un objeto cualquiera, se puede decidir si ese objeto es un elemento del conjunto o no.
Cardinal de un conjunto
El cardinal de un conjunto A es el número de elementos que tiene dicho conjunto. A ese número lo denotaremos por | A |.
Subconjuntos e Inclusión
Sea A un conjunto. Se dice que un conjunto
B esta contenido en A, y se nota B ⊆ A (o también B ⊂ A), si todo elemento de B es un elemento de A. En ese caso decimos también que b esta incluido en A, o que B es un subconjunto de A.
Si B no es un subconjunto de A se nota B ̸⊆ A (o B ̸⊂ A)
igualdad de conjuntos
Es decir A = B si tienen exactamente los mismos elementos (sin importar el orden y sin tener en cuenta repeticiones de elementos). (Aquí, el símbolo “⇔” es el símbolo de la bi-implicacion,
que se lee “si y solo si”.)
Operaciones entre conjuntos
Supondremos en todo lo que sigue que los conjuntos A, B, C, . . . que se consideran son subconjuntos de un mismo conjunto referencial (o de referencia) U (para poder “operar”). Esto también es generalmente indispensable al definir un conjunto por comprensión, como por ejemplo P = {n ∈ N : n es un numero par }, o I = {x ∈ R : x ≤ 2} = [−∞, 2), que no es lo mismo
que J = {x ∈ N : x ≤ 2} = {1, 2}.
relaciones
Sean A y B conjuntos. Un subconjunto R del producto cartesiano A × B se llama una relacion de A en B. Es decir R es una relacion de A en B si R ∈ P(A × B).
Funcion
Sean A y B conjuntos, y sea R una relacion de A en B. Se dice
que R es una función cuando todo elemento a ∈ A esta relacionado con algún b ∈ B, y este elemento b es único
Una función es inyectiva cuando a diferentes elementos del dominio le corresponden distintos elementos del codominio, y recíprocamente, a distintos elementos del codominio se le asocian diferentes elementos del dominio. También se le conoce como función uno a uno.
Una función es suprayectiva si cualquier elemento del codominio es imagen de por lo menos un elemento del dominio de la función. También se le conoce como sobreyectiva.
Una función es biyectiva si cumple con ser inyectiva y suprayectiva. La regla de correspondencia es
biunívoca.