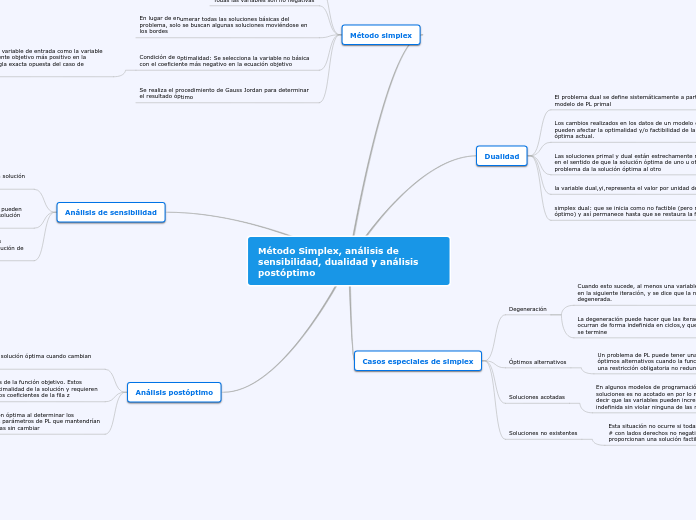
Método Simplex, análisis de sensibilidad, dualidad y análisis postóptimo
Dualidad
El problema dual se define sistemáticamente a partir del modelo de PL primal
Los cambios realizados en los datos de un modelo de PL pueden afectar la optimalidad y/o factibilidad de la solución óptima actual.
Las soluciones primal y dual están estrechamente relacionadas en el sentido de que la solución óptima de uno u otro problema da la solución óptima al otro
la variable dual,yi,representa el valor por unidad del recurso i.
simplex dual: que se inicia como no factible (pero mejor que óptimo) y así permanece hasta que se restaura la factiblidad
Casos especiales de simplex
Degeneración
Cuando esto sucede, al menos una variable básica será cero en la siguiente iteración, y se dice que la nueva solución está degenerada.
La degeneración puede hacer que las iteraciones simplex ocurran de forma indefinida en ciclos,y que el algoritmo nunca se termine
Óptimos alternativos
Un problema de PL puede tener una cantidad infinita de óptimos alternativos cuando la función objetivo es paralela a una restricción obligatoria no redundante
Soluciones acotadas
En algunos modelos de programación lineal,el espacio de soluciones es no acotado en por lo menos una variable, es decir que las variables pueden incrementarse de forma indefinida sin violar ninguna de las restricciones
Soluciones no existentes
Esta situación no ocurre si todas las restricciones son del tipo # con lados derechos no negativos porque las holguras proporcionan una solución factible obvia
Método simplex
Todas las restricciones son ecuaciones con el lado derecho no negativo
Todas las variables son no negativas
En lugar de enumerar todas las soluciones básicas del problema, solo se buscan algunas soluciones moviéndose en los bordes
Condición de optimalidad: Se selecciona la variable no básica con el coeficiente más negativo en la ecuación objetivo
drequiere seleccionar la variable de entrada como la variable no básica con el coeficiente objetivo más positivo en la ecuación objetivo, la regla exacta opuesta del caso de maximización
Se realiza el procedimiento de Gauss Jordan para determinar el resultado óptimo
Análisis de sensibilidad
El cual determina las condiciones que mantendrán la solución actual sin cambios.
Condición de factibilidad: Tanto en problemas de maximización como de minimización,la variable de salida es la variable básicaasociada con la relación mínima no negativa con el denominador estrictamente positivo.
En PL,los parámetros (datos de entrada) del modelo pueden cambiar dentro de ciertos límites sin que cambie la solución óptima
el análisis de sensibilidad gráfica para determinar las condiciones que mantendrán la optimalidad de la solución de una PL de dos variables.
Análisis postóptimo
el cual determina la nueva solución óptima cuando cambian los datos del modelo.
Cambios en los coeficientes de la función objetivo. Estos cambios afectan sólo la optimalidad de la solución y requieren que se calculen de nuevo los coeficientes de la fila z
la sensibilidad de la solución óptima al determinar los intervalos de los diferentes parámetros de PL que mantendrían las variables básicas óptimas sin cambiar