MATEMÁTICAS CERCANAS
¿PARA QUÉ ESTUDIAR
LOGARITMOS?
Conocer y comprender la historia de los logaritmos
nos ayuda a definir los logaritmos. Saber exacta_
mente que pensaban nuestros antepasados y que
necesidades tuvieron para plantearlos, nos sirve para ponernos en el lugar del otro y valorar los avances tecnológicos, que actualmente hacen tan sencilla
nuestra tarea.
ACTIVIDAD N° 1
Buscar información sobre la historia del logaritmo
-¿Quién lo plantea?
-¿Por qué?
- ¿En respuesta a qué necesidad?
-¿Con el avance de la tecnología qué se logró?
-¿Cuál es la definición de logaritmo?
- ¿Cuáles son los beneficios de tener una calculadora
científica?¿Son todas igual?¿Qué diferencias encontraron?
Estas son algunas de las preguntas que se le propone responder a los estudiantes en la guía que se les entregará.
ACTIVIDAD N° 2
En la sala de informática elaboraron un rosco
con los contenidos trabajados de logaritmos.
ACTIVIDAD N° 3
Abordamos la propiedades de los logaritmos.
Reforzamos sus aplicaciones utilizando Kahoot
ACTIVIDAD N° 4
Las ecuaciones exponenciales y logarítmicas se ven
aplicadas a la realidad y a su perfil de egresados.

LOS POLINOMIOS
EN LA VIDA DIARIA
Infinitas son las aplicaciones que encontramos
de polinomios en las ciencias, de esto se trata
este curso de ver su en el mundo
que nos rodea
ACTIVIDAD N° 1
Buscar información sobre la aplicación de polinomios.
- Escoger un ejemplo.
-Encontrar sus características: grado, coeficiente principal, termino independiente, raíces y nombre.
Ejemplo 1
Ejemplo 2
ACTIVIDAD N° 2
Se les solicita ver los siguiente video
para poder encontrar las raíces del
polinomio elegido en la actividad 1.
ACTIVIDAD N° 3
Abordamos los 7 casos de factoreo.
Reforzamos sus aplicaciones utilizando Kahoot
¿QUÉ UTILIDAD TIENE
LAS EXPRESIONES ALGEBRAICAS
FRACCIONARIAS?
En estos ejercicios se utilizan los Casos de Factoreo de Polinomios, se opera con polinomios (suma, resta y multiplicación), y se calcula el Mínimo Común Múltiplo entre polinomios (m.c.m). También se resuelven ecuaciones de grado 1 y ecuaciones cuadráticas. Por lo tanto utilizaremos las
capacidades adquiridas en la unidad anterior.
ACTIVIDAD N° 1
Reconocimiento y uso de las
operaciones entre expresiones
algebraicas racionales en situaciones
problemáticas que requieran:
interpretación de modelos que den
significado a la suma, resta,
multiplicación y división. Para ello se
les propone visitar el link:
https://www.sangakoo.com/es/temas/problemas-de-aplicacion-de-polinomios-y-fracciones-algebraicas
ACTIVIDAD N° 2
A partir del análisis de casos de la actividad anterior
elaboren un mapa mental explicando cada una de las
operaciones entre expresiones algebraicas fraccionarias.
ACTIVIDAD N° 3
Trabajaran en grupo. Cambio de roles.
Buscarán dos maneras diferentes de resolver correctamente ecuaciones algebraicas fraccionarias. Expondrán cada caso. Cumplirán por un día el rol de docentes, explicándole a sus
compañeros los resultados obtenidos.
¿ES LA TRIGONOMETRÍA
LA SOLUCIÓN A MUCHOS
PROBLEMAS DE LA ARQUITECTURA
Y OTRAS RAMAS?
ACTIVIDAD N° 1
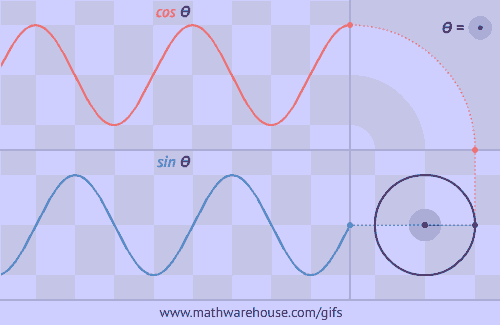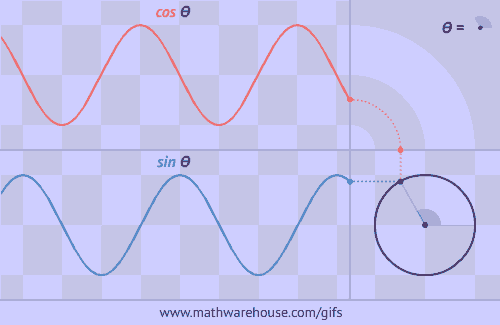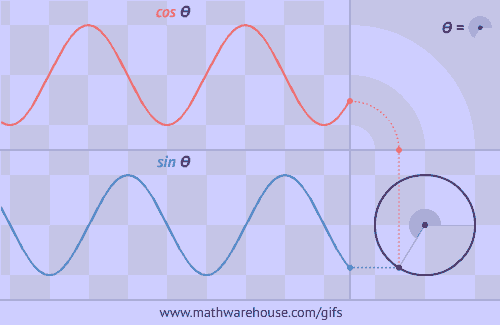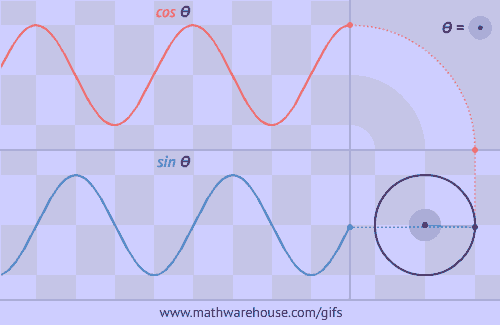
Buscarán información sobre los distintos sistemas de medida de ángulos.Luego utilizando la aplicación geogebra realizaran un reconocimiento de los ángulos en los distintos sistemas. Graficarán las funciones seno, coseno y tangente para realizar una comparación entre ellas y sus distintos elementos.
ACTIVIDAD N° 2

Resolución de triángulo rectángulos, si de aplicar a la
realidad se trata este tema es especial. Por ellos se les
pedirá a los alumnos que resulvan situaciones puntuales
de la vida cotidiana y otras relacionadas a su perfil
profesional.
ACTIVIDAD N° 3

La aplicación se amplía a los triángulo
oblicuángulos. Se les solicita a los estudiantes
ver el video, para luego por aplicar los teoremas
a otros casos particulares.
