Math156
Problem Solving
George Poylas 4 steps
Step 1. Understand the problem
Step 2. Devising a plan
Step 3. Carrying out the plan
Step 4. Looking back
Sum of sequential numbers
n(n+1)/2
Arithmetic Sequence
Addition of subtraction of a fixed number
Fibonacci Sequence
Sequence when the sum of the first two numbers becomes the third number, and so on. ex 1,1,2,3,5,8,13,21...
Geometric Sequence
Each successive term of a geometic sequence is obtained from its predecessor by multiplying by a fixed number, the ratio. (Ratio can never =0) ex2,4,8,16,32...
Numeration Systems
Hindu-Arabic
All numbers come from the 10 digits (0,1,2,3,4,5,6,7,8,9)
Tally Numberation System
This method uses single strokes or tally marks to represent each item being counted. ( l,ll,lll)
Roman Numeration System
l=1, V=5, X=10, L=50, C=100, D=500, M=1000
Base Five
Sets
One to One Correspondence
If the elements of sets P and S can be paired so that each element of P there is exactly one element of S, then the two sets P and S are considered one to one correspondence
Equivalent Sets
Two sets A and B are equivalent, if and only if there exists a one-to-one correspondence between the sets.
Cardinal Numbers
The cardinal number of a set denotes the number of elements in a set. ex. (a,b) (r,s),@,#) are equivalent to each other because they each have two elements in their set.
Universal Set
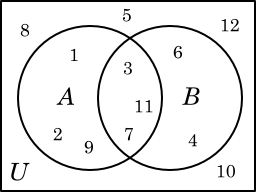
Universal set denoted U, is the set that contains all the elements being considered in a discussion. A Venn diagram can be used to illustrate sets.
Subset
B is a subset of A, if every element of B is an element of A.
Set Intersection
The intersection of two sets, A and B, is the set of all elements common to both A and B.
Set Union
The union of two sets A and B, is the set of all elements in A or B.
Set Difference
The colplement of A relative to B, is the set of all elements in B that are not in A.
Properties of Set Opperations
1. Associative Property 2. Distributive Property
Cartesian Pruducts
For any sets A and B, the Cartesian produce of A and B, is the set of all ordered pairs such that the first componet of each pair is an element of A and the second componet of each is an element of B.
Operations
Vocabulary
Addends: Numbers added together
Sum: Total number after adding two or more numbers
Dividend: A number divided by another
Divisor: A number by which another number is to be divided
Quotient: The answer after dividing one number into another
Difference: The result of subtracting one number from another.
Product: The result of multiplying two or more numbers
Multiplication: An operation that gives the total number when you join two or more numbers
Subtraction: The operation of taking away/subtracting two or more numbers.
Addition: The opperation of adding two or more numbers.
Division: The operation of dividing multiple numbers into each other.
Function: A relation in which every input value is paired with exactly one output value.
Relations: A set of input and output values. Usually represented in ordered pairs.
Functions
Ordered pairs
The rule
Make table
Make a graph
Arrow diagram
Teaching Addition and Subtraction Facts
Numbers Blocks
Counting On
Number Line
Fact Family
Counting Backwards
Counting by 10s
Countin by Doubles
Order of Operation
Parenthesis
Exponents
Division
Multiplication
Addition
Subtraction
Order of Long Division
Divide
Multiply
Subtract
Check
Bring Down
Correct/Circle
Properties
Distributive: a(b+c) =ab+ac
Associative: a+(b+c)=(a+b)+c
Commutaive: a+b=b+a
Closure: The set of whole numbers is closed under multiplication.
Identity: Any number multiplied by 1 is the same number 2x1=2
Zero multiplication: Any number multiplied by 0 is 0 2x0=0
Integers
Integer Addition
1. Chip model
2. Number line
3. Absolute value
Closure property
Communitive property
Associative property
Identity property
Integer Subtraction
1. Chip model
2. Number line
3. Pattern model for subtraction
Adding opposites: "Keep change change"
Missing addends
Integer Multiplication
Multiply a positive and a positive the answer is positive
Multiply a positive and a negative the answer is negative
Integer Division
Divide a positive and a positive the answer is positive
Divide and positive and a negative the answer is negative
Divisibility
A number is divisible by 2 if the number ends with an even number. ex. 202
A number is divisible by 3 if the sum of the digits is divisible by 3. ex. 123
A number is divisible by 4 if the last two digits are divisible by 4. ex 424
A number is divisible by 5 if the number ends with 0 or 5. ex. 205
A number is divisible by 6 if the number is divisible by both 2 and 3. ex. 126
A number is divisible by 8 if the last 3 digits are divisible by 8. ex. 1,888
A number is divisible by 9 if the sum of digits is divisible by 9. ex. 126
A number is divisible by 10 if the number ends with 0. ex. 200
A number is divisible by 11 if the sum of the digits in the places that are even powers of 10 minus the sum of the digits in the places that odd powers of 10 is divisible by 11. ex. 57,729,364,583
Prime numbers
Prime numbers are numbers that only have 2 factos or positive divisors. ex. 2,3,5,7,11,13,17,19
Composite numbers
Composite numbers are numbers that have more than 2 factors or positive divisors. ex. 4,6,8,9,10,12,14,15,16,18,20
Greatest Common Divisor
The greatest common divisor of two natural numbers a and b is the greatest natural number that divides both a and b.
1. The intersection of Sets Method
2.Prime factorization method
3. Ladder method
Least Common Multiple
The least common multiple of a and b is the least natural number that is simultaneously a multiple of a and multiple of b.
1. Number line method
2. Intersection of Sets Method
3. Prime factorization method
4. Ladder method
Fractions and Decimals

Adding fractions
Subtracting fractions

Multiplying fractions

Dividing fractions

Adding decimals

Subtracting decimals

Multiplying decimals

Dividing decimals
Scientific Notation: Used when you have either a very large or small number. EX large: 93,000,000=9.3x10power of 7 EX small: 0.000078=7.8x10-power of 5.

Subtopic