MATH'S PROGRAM
GONIOMETRIA
gli angoli e le loro misure
angolo
angoli associati

tabella:)
le funzioni goniometriche
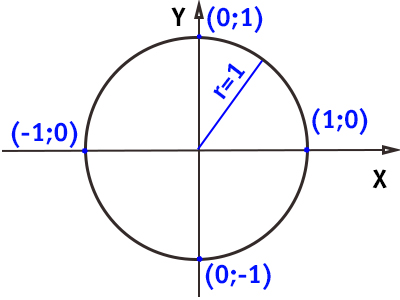
La circonferenza goniometrica è una circonferenza di
raggio unitario (R = 1) con centro nell'origine degli assi
cartesiani x e y.
:)
seno di α l'ordinata di P
VARIAZIONE DELLE FUNZIONI SENO E COSENO
coseno di α l'ascissa di P
tanα= sinα/cosα
l'ascissa del punto d'intersezione tra la tangente geometrica alla circonferenza goniometrica nel punto di origine degli angoli eil lato terminale dell'angolo stesso
cotgα = cosα/sinα
è l'ordinata del punto d'intersezione tra la tangente geometrica alla circonferenza goniometrica nell'estremo del primo quadrante e il lato terminale dell'angolo stesso
proprietà delle funzioni goniometriche
sin^2α+cos^2α=1
è una relazione che lega il seno e il coseno di uno stesso angolo. In base ad essa sappiamo che la SOMMA dei quadrati del seno e del coseno di uno stesso angolo sono sempre UGUALI all'UNITA'.
tanα=sinα/cosα
mette in relazione le funzioni tangente, seno e coseno
grafici
y=sinx
y=cosx
y=tanx
elementari
solo con una funzione goniometrica di I grado
riconducibili ad elementari
non sembrano elementari ma sono facilmente riconducibili a esse
di secondo grado
con una o più funzioni goniometriche al quadrato
lineari
sin e cos entrambi non elevati a potenza
in seno e coseno
per risolverle si può utilizzare o il metodo geometrico o algebrico
formule goniometriche
addizione o sottrazione
ci consentono di esprimere il sin e cos della somma o differenza di due angoli in funzione del sin e cos, dei singoli angoli coinvolti
duplicazione
bisezione
clicca sul link affianco per visualizzare le varie formule in un unico schema :)→
parametriche
werner (prodotto-somma)
prostaferesi (somma-prodotto)
disequazioni
disequazioni goniometriche elementari o a esse riconducibili
disequazioni goniometriche elementari
del tipo sin x>m, con m>0
sinx≥m, con m<0
possono essere risolte utilizzando due metodi
utilizzando la circonferenza goniometrica
utilizzando il grafico y=sinx
cosx<m
tanx≤m
riconducibili a goniometriche elementari
mediante sostituzione
riconducibili a disequazione di secondo grado in coseno
frazionarie e prodotto
f(x)/g(x)>0
lineari in seno e coseno
asinx + bcosx + c >0
omogenee di secondo grado in seno e coseno
asin^2x + bsinx cosx + ccos?2x>0
TRIGONOMETRIA
La trigonometria studia i rapporti tra le misure degli
angoli e la lunghezza dei lati di un triangolo. Essa confronta le lunghezze dei lati di triangoli rettangoli simili (che hanno la stessa forma ma misure diverse) per trovare la misura degli angoli e dei lati non noti.
teoremi sui triangoli rettangoli
primo teorema
in un triangolo rettangolo la misura di un cateto è uguale a quella dell'ipotenusa moltiplicata per il seno dell'angolo opposto al cateto, o moltiplicata per il coseno dell'angolo acuto adiacente al cateto.
b=αsinβ oppure b=αcosγ
c=αcosβ oppure c=αsinβ

visualizza la figura per capire meglio!
secondo teorema
in un triangolo rettangolo la misura di un cateto è uguale a quella dell'altro cateto moltiplicata per la tangente dell'angolo opposto al primo cateto, o moltiplicata per la cotangente dell'angolo acuto adiacente al primo cateto.
b= ctanβ oppure b=ccotγ
c=btanγ oppure c=bcotβ
teoremi triangoli
teorema dell'area
L’area di un triangolo qualsiasi è uguale al semiprodotto delle misure di due suoi lati per il seno dell’angolo fra essi compreso.
teorema della corda
In una circonferenza la misura di una corda è uguale al prodotto della misura del diametro per il seno di uno degli angoli alla circonferenza che insistono sulla corda.
AB=2r sinα
AB=2r sin (180-α)
teorema dei seni
In un triangolo qualunque è costante il rapporto tra la misura di un lato e il seno dell’angolo opposto
:)
teorema del coseno
In un triangolo qualsiasi il quadrato di un lato è uguale alla somma dei quadrati degli altri due diminuita del doppio prodotto di questi due lati per il coseno dell’angolo fra essi compreso
a²= b² + c² - 2bc cosα
c²= a²+ b² - 2ab cosγ
risoluzione di un triangolo qualsiasi
sono noti un lato del triangolo e i due angoli adiacenti
sono noti due lati del triangolo e l'angolo compreso fra di essi
video per capire meglio :)
sono noti i tre lati del triangolo
sono noti due lati del triangolo e un angolo non compreso tra di essi