Vectores en el espacio
Definición de vector

Es un ente matemático como la recta o el plano. Un vector se representa mediante un segmento de recta, orientado dentro del espacio euclidiano tridimensional. El vector tiene 3 elementos: módulo, dirección y sentido. Los vectores nos permiten representar magnitudes físicas vectoriales, como las mencionadas líneas abajo.
Módulo o tamaño de un vector
En física, se llama módulo de un vector a la norma matemática del vector de un espacio euclídeo ya sea este el plano euclídeo o el espacio tridimensional. El módulo de un vector es un número que coincide con la "longitud" del vector en la representación gráfica.
El concepto de norma de un vector generaliza el concepto de módulo de un vector del espacio euclídeo.

Cálculo

Dado un vector del espacio euclídeo tridimensional expresado por sus componentes, su módulo es el número real dado por la expresión.

Propiedades
Relación con el producto escalar: El módulo de la suma de dos vectores está relacionado con el producto escalar y los módulos respectivos de los vectores

Desigualdad triangular: El módulo de la suma de dos vectores es menor o igual que la suma de módulos.

Ejes de coordenadas
Lo forman dos ejes perpendiculares entre sí, que se cortan en el origen.


Los ejes de coordenadas dividen al plano en cuatro partes iguales y a cada una de ellas se les llama cuadrante

El eje horizontal se llama eje X o eje de abscisas.
El eje vertical se llama eje Y o eje de ordenadas.
El punto O, donde se cortan los dos ejes, es el origen de coordenadas.
Las coordenadas de un punto cualquiera P se representan por (x, y).
Ángulos directores
Se llaman ÁNGULOS DIRECTORES de un vector, a los ángulos que el vector forma con las direcciones positivas de los ejes coordenados. Estos ángulos deberán ser tomados entre 0 y π (0º y 180º).
Si el vector V está en R3 y sus componentes son: (v1, v2, v3) tiene tres ángulos directores: α (ángulo formado con la dirección positiva del eje x); β (ángulo formado con la dirección positiva del eje y) y γ (ángulo formado con la dirección positiva del eje z).

Formas de expresar un vector y vector unitario
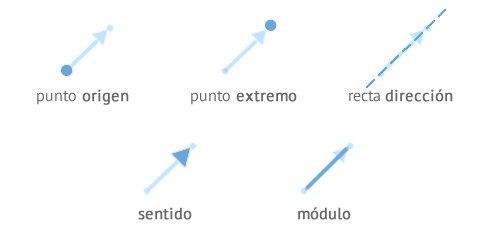
Gráficamente, un vector se representa como una flecha ubicada en un eje de coordenadas. En esta flecha podemos identificar cada uno de los elementos que lo conforman y que estudiamos en el apartado anterior, además de algunos más.
Datos Iniciales
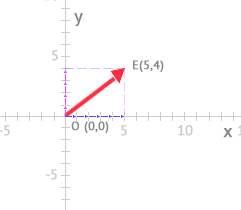
a→= 5 ⋅ i→+ 4 ⋅ j→
Desarrollo de la solución
Dado que la ecuación de un vector es de la forma a→= ax ⋅ i→+ay ⋅ j→
podemos ver claramente que las componentes cartesianas del vector a son ax = 5 y ay = 4. Si aplicamos la fórmula para calcularlas:
ax=Bx−Ax
ay=By−Ay
y despejamos Ex y Ey y sustituimos el resto de valores:
Ex=ax+Ox ⇒ Ex = 5 + 0 ⇒Ex= 5Ey=ay+Oy ⇒ Ey = 4 + 0 ⇒Ey= 4E = (Ex, Ey) ⇒ E = (5,4)
por lo tanto tenemos que el vector a tiene como punto de origen O(0,0) y como punto de extremo E(5,4). Ya solo queda representarlo en el eje de coordenadas.
Solución