producto cartesiano
Topic principal
El nombre producto cartesiano fue puesto en honor al matemático, fısico y filósofo francés
René Descartes, 1596-1650
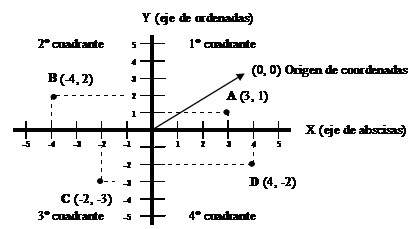
Subtopic
Representación

diagrama de venn
Relacion
Relación entre conjuntos
Se llama una relación R entre conjuntos A y B a un subconjunto del producto cartesiano A x B, de tal modo que (x; y) Ꞓ R si y únicamente si x está relacionado y por la relación.

Representaciones de relaciones
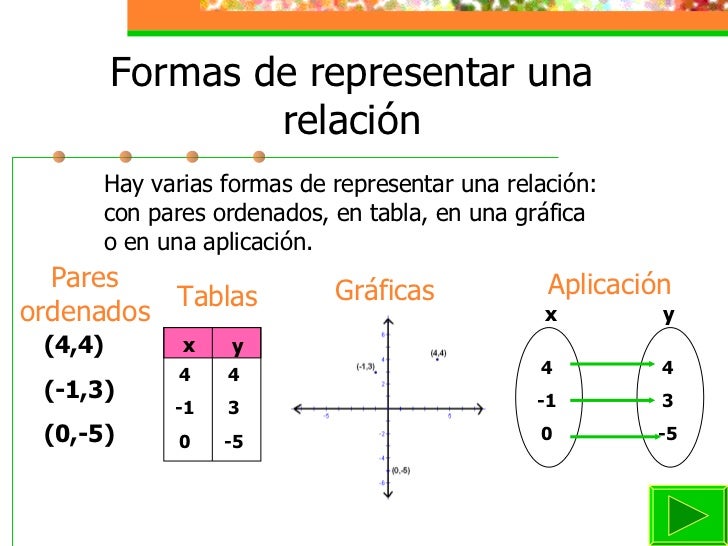
Subtopic
RELACION DE EQUIVALENCIA
relacion entre conjunto
REFLEXIVA
SIMETRICA
ANTISIMETRICA
TRANSITIVA
CLASES DE EQUIVALENCIAS
RELACION DE ORDEN
POR EXTENSION
POR COMPRENCION
A x B = {(x,y) / x Ꞓ A ᴧ y Ꞓ B }
Bueno damos finalizado brevemente el tema dando paso al proximo tema