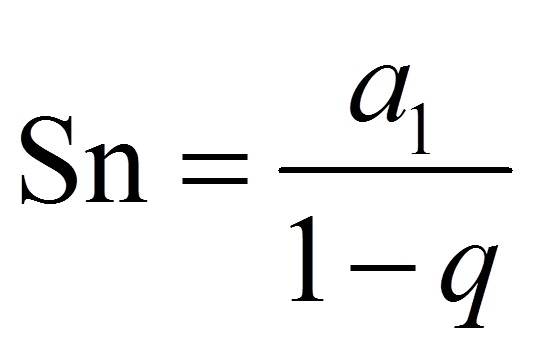Progressão Geométrica
(PG)
Definição
PG é uma sequência em que cada termo, a partir do segundo, é o produto do termo anterior por uma contante q.
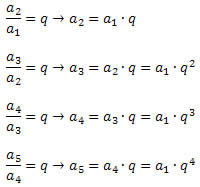
Classificação
Crescente
q >1 e a1 > 0 , Ex.: (2, 4, 8, 16, 32)
ou
0 < q < 1 e a1 < 0 , Ex.: (-8, -4, -2, -1)
Decrescente
q > 1 e a1 < 0 , Ex.: (-8, -16, -32, -64)
ou
0 < q < 1 e a1 > 0, Ex.: (81, 27, 9, 3, 1)
Oscilante
q < 0, Ex.: (5, -15, 45, -135)
Constante
q = 1, Ex.: (4, 4, 4, 4)
Estacionária
q = 0, Ex.: (3, 0, 0, 0)
Notações especiais
3 termos
(x, x.q, x.q²) ou (x/q, x, x.q)
4 termos
(x, x.q, x.q², x.q³)
ou
fazendo q = y²
(x/y³, x/y, x.y, x.y³)
5 termos
(x, x.q, x.q², x.q³, x.q^4)
ou
(x/q², x/q, x, x.y, x.y²)
Fórmula do termo geral
Produto dos termos de uma PG
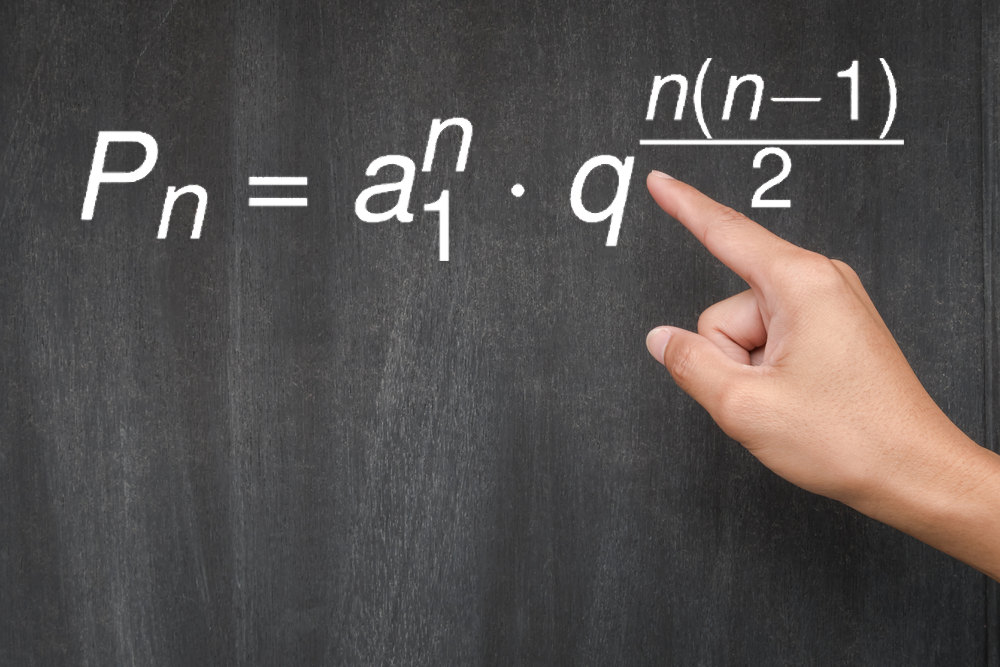
Soma dos termos de uma PG
PG Finita
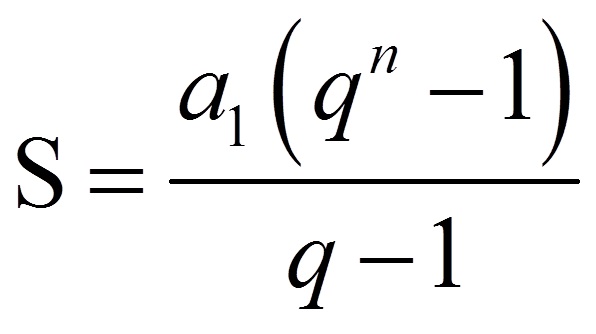
PG Infinita