RECTAS Y PLANOS EN EL ESPACIO
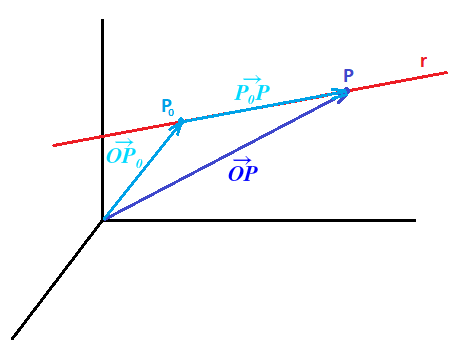
LA RECTA EN EL ESPACIO
Ecuación vectorial
determinada por
un punto (P)
un vector (V)
vector
de posición (OP)
director (V)
vector OP+t·v
origen en O
extremo es un punto de la recta r
(x,y,z)=(x0,y0,z0)+t(v1,v2,v3)
Ecuaciones paramétricas
igualando coordenada a coordenada
x=x0+t·v1 y=y0+t·v2 z=z0+t·v3
Ecuación continua
despejando t e igualando
t= x-x0/v1=y-y0/v2=z-z0/v3
Ecuaciones implícitas o cartesianas
separando las igualdades y agrupando todos los términos en un mismo miembro
Ax+By+C=0 A'x+B'z+C=0

ECUACIONES DEL PLANO EN EL ESPACIO
Ecuación vectorial del plano
determinado por
un punto (P)
dos vectores directores (u) y (v)
vector OP+λ·u+μ·v
origen en O
el extremo es un punto del plano π
(x,y,z)=(x0,y0,z0)+λ·(u1,u2,u3)+μ·(v1,v2,v3)
Ecuaciones paramétricas del plano
igualando coordenada a coordenada
x=x0+λ·u1+μ·v1 y=y0+λ·u2+μ·v2 z=z0+λ·u3+μ·v3
Ecuación general del plano
sólo dos de los tres vectores son linealmente independientes
Si el Rg=2
no será posible encontrar un menor de orden 3 no nulo
determinante de la matriz=0
desarrollando la matriz se obtienen cuatro valores reales
Ax+By+C+D=0
vector normal del plano
π:Ax+By+C+D=0
n=(A,B,C)
perpendicular al plano

POSICIONES RELATIVAS
Posiciones relativas de dos planos en el espacio
sean los planos π y π'
π: Ax+By+Cz+D=0
π':A'x+B'y+C'z+D'=0
sistema formado por ambas ecuaciones
Ax+By+Cz+D=0 A'x+B'y+C'z+D'=0
M
matriz de coeficientes
M*
matriz ampliada con los términos independientes
rango de M y M*
rg (M ) = rg (M *) = 1 < nº incógnitas⇒ S.C.I.
infinitas soluciones
planos coincidentes
Rg=1 si las dos filas de M y * M son
proporcionales
simplificando una de las ecuaciones puede obtenerse la otra
rg (M ) = 1 ≠ rg (M *) = 2 ⇒ S.I.
no tiene solución
planos paralelos
RgM=1 si las filas son proporcionales
rg (M ) = rg (M *) = 2 < no incógnitas ⇒ S.C.I.
infinitas soluciones
planos secantes
su intersección es una recta
Posiciones relativas de tres planos en el espacio
sean los planos π, π' y π"
π: Ax+By+Cz+D=0
π':A'x+B'y+C'z+D'=0
π":A"x+B"y+C"z+D"=0
sistema formado por ambas ecuaciones
Ax+By+Cz+D=0 A'x+B'y+C'z+D'=0 A"x+B"y+C"z+D"=0
rango de M y M*
rg (M ) = rg (M *) = 1 < no incógnitas ⇒ S.C.I.
ecuaciones proporcionales
infinitas soluciones
tres planos coincidentes
Rg=1 si las tres filas de M y * M son
proporcionales
rg (M ) = 1 ≠ rg (M *) = 2 ⇒ S.I.
dos ecuaciones son proporcionales y la otra no
dos planos coincidentes y paralelos al
tercero
Rg=1
vectores ortogonales proporcionales
planos paralelos
plano
no coincidente
el término D no es proporcional a los otros dos
ninguna de las ecuaciones es proporcional
tres planos paralelos
rg (M ) = rg (M *) = 2 < no incógnitas ⇒ S.C.I.
dos de las ecuaciones son proporcionales
dos planos coincidentes que cortan al
tercero
no hay ecuaciones proporcionales
los tres planos se cortarán
en una recta
rg (M ) = 2 ≠ rg (M *) = 3 ⇒ S.I.
dos de los planos son paralelos
cortan al tercero
ninguno de los planos es paralelo al otro
se cortan dos a dos y definen un prisma sin bases
rg(M ) = rg(M *) = 3 ⇒ S.C.D.
única solución
los tres planos se cortan en un punto
Posiciones relativas de una recta y un plano en el espacio
ecuaciones implícitas y un plano π
Ax+By+Cz+D=0 A'x+B'y+C'z+D'=0
π":A"x+B"y+C"z+D"=0
sistema formado por las ecuaciones de la recta y el plano
rango de M y M*
rg (M ) = rg (M *) = 2 ⇒ S.C.I.
infinitas soluciones
recta contenida en un plano
rg (M ) = 2 ≠ rg (M *) = 3 ⇒ S.I.
no tiene solución
recta y plano no se cortan
paralelos
Si rg (M ) = rg (M *) = 3 ⇒ S.C.D.
única solución
recta y plano se cortan en un punto
secantes
Posiciones relativas de dos rectas en el espacio
ecuaciones implicitas
Ax+By+Cz+D=0 A'x+B'y+C'z+D'=0
A"x+B"y+C"z+D"=0 A"x+B"y+C"z+D"=0
sistema formado por cuatro ecuaciones
rango de M y M*
rg (M ) = rg (M *) = 2 ⇒ S.C.I.
infinitas soluciones
rectas coincidentes
sólo dos de
las ecuaciones son linealmente independientes
rg (M ) = 2 ≠ rg (M *) = 3 ⇒ S.I.
no tiene solución
vectores directores proporcionales
rectas paralelas
rg (M ) = rg (M *) = 3 ⇒ S.C.D.
única solución
rectas secantes
intersección un punto
rg (M ) = 3 ≠ rg (M *) = 4 ⇒ S.I.
no tiene solución
vectores directores no son proporcionales
las dos rectas se cruzan