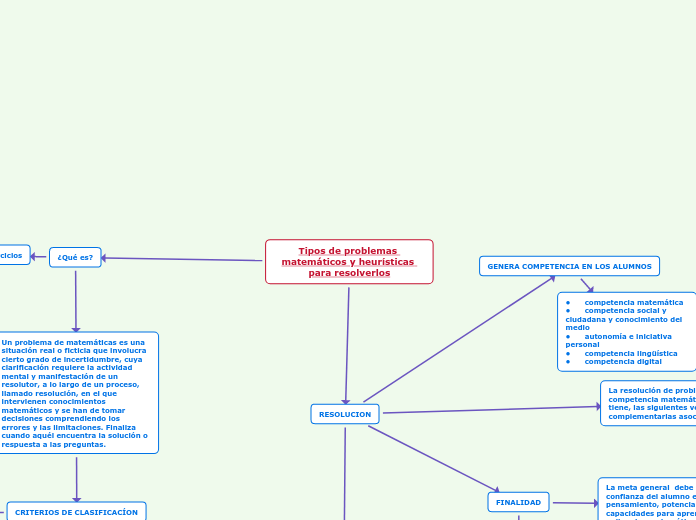
Tipos de problemas matemáticos y heurísticas para resolverlos

¿Qué es?

Un problema de matemáticas es una situación real o ficticia que involucra cierto grado de incertidumbre, cuya clarificación requiere la actividad mental y manifestación de un resolutor, a lo largo de un proceso, llamado resolución, en el que intervienen conocimientos matemáticos y se han de tomar decisiones comprendiendo los errores y las limitaciones. Finaliza cuando aquél encuentra la solución o respuesta a las preguntas.

CRITERIOS DE CLASIFICACÍON

• Su ámbito o entorno en el que aparecen
• Su estructuración
• Su presentación
• Los problemas de enunciado verbal
• Su solución
• Su proceso de resolución

TIPOS MAS FRECUENTES

• Problemas de enunciado verbal(los clásicos escolares)
 Problemas aritméticos
 Problemas geométricos
 Problemas de azar y probabilidad
• Problemas de razonamiento lógico
• Problemas manipulativos (material didáctico)
• Problemas ligados a juegos y pasatiempos
• Problemas de modelización matemática

diferencias con ejercicios

ejercicio:
• Tarea escolar
• La finalidad educativa es la de entrenamiento y consolidación de contenidos explicados, aprendidos o en vías de aprendizaje y a veces de evaluación o comprobación de su aprendizaje
• Es una tarea repetitiva, rutinaria, de resultados previsibles (aunque hay que saber cómo se hace)
• Generalmente tienen solución única
• Se realizan o completan en un tiempo corto

Problema:
• Tarea escolar o extraescolar
• La finalidad educativa es proporcionar experiencias sobre la utilidad y las aplicaciones del conocimiento matemático, desarrollar las competencias básicas y evaluarla disponibilidad del conocimiento ante situaciones en las que es útil
• Siempre supone un reto, una actividad desconocida, apasionante y de resultados imprevisibles
• Generalmente tienen solución única
• Suelen requerir más tiempo.

RESOLUCION

No existe un método universal pararesolver problemas de matemáticas, sino enfoques, experiencias, estrategias y técnicas de resolución y orientaciones que pueden ayudar en dicha tarea. Son especialmente útiles las etapas o fases y las herramientas y técnicas heurísticas que establecen distintos autores

ETAPAS O FASES

Polya (1945)y Echenique (2006)identificanlas siguientes etapas:
• COMPRENSIÓN del problema
• PLANIFICACIÓN o Concepción de un plan
• EJECUCIÓN del plan
• VALORACIÓN de la respuesta y del proceso seguido

Barnsford y Stein (1984) proponen un método con 5 fases cuyas iniciales forman la palabra IDEAL, especialmente útil para los problemas relacionados con situaciones reales.
• I Identificación
• D Definición y representación
• E Exploración de posibles estrategias
• A Actuación fundada en una estrategia
• L Logros. Observación y evaluación de los efectos de nuestras actividades.

Puig y Cerdán (1988) proponen las siguientes fases para la resolución de problemas aritméticos:
• Lectura
• Comprensión
• Traducción
• Cálculo
• Solución
• Revisión y comprobación

HERRAMIENTAS / TÉCNICAS HEURÍSTICAS

• Para comprender el problema: Repetirlo en voz alta o explicárselo a otras personas; buscar analogías o semejanzas, analizar las dificultades; representar y organizar la información
• Para representar y organizar la información: identificar y distinguir la información; codificar, representar y organizar la información, separar lo que se sabe de lo que no se sabe y lo que hay que averiguar o pide el problema
• Paraplanificar o idear un plande resolución: explorar, generalizar, conjeturar y comprobar, experimentar, modificar el problema, técnicas matemáticas usuales.

EURISTICA

La heurística es el estudio de los modos de comportamiento al resolver problemas y los medios que se utilizan, que son independientes del contenido y que no suponen garantía de que se obtenga la solución

FINALIDAD

la resolución de problemas de matemáticas es el campo del aprendizaje matemático y debe constituir una parte fundamental de la metodología de la enseñanza de esta materia.

La meta general debe ser la de mejorar la confianza del alumno en su propio pensamiento, potenciarlas habilidades y capacidades para aprender, comprender y aplicar las matemáticas

GENERA COMPETENCIA EN LOS ALUMNOS

• competencia matemática
• competencia social y ciudadana y conocimiento del medio
• autonomía e iniciativa personal
• competencia lingüística
• competencia digital

La resolución de problemas es una competencia matemática específica que tiene, las siguientes vertientes complementarias asociadas a su desarrollo:

• Planificación:
Conjunto de capacidades asociadas a la comprensión de la situación planteada para organizar, trazar un plan, buscar estrategias y tomar decisiones

• gestión de los recursos:
El alumno tiene una serie de destrezas y conocimientos básicos previos para afrontar la resolución de un problema y gestionar bien y de manera organizada dichos recursos a lo largo de todo el proceso y no sólo en la fase de ejecución

• Representación
Las capacidades y destrezas relacionadas con la representación son:
-En la fase de comprensión: lectura comprensiva, representar mediante esquemas, palabras, símbolos, etc.
-En la fase de planificación: esquemas, diagramas, dibujos, pasos a seguir, organizar y codificar.
-En la fase de ejecución: realizar y escribir cálculos y relaciones y estructurar pasos y resultados.
-En la fase de valoración: repetir los pasos contando con las soluciones encontradas, reflexionar mediante un esquema del proceso seguido, utilizar otros datos y comprobar si hay más resultados.

• Interpretación y valoración global de los resultados
-Comprobación de la bondad de la respuesta y la coherencia de todo el proceso
-Análisis de procedimientos y resultados alternativos
-Análisis de dificultades