av Joss Ivonne Lans för 4 årar sedan
1809
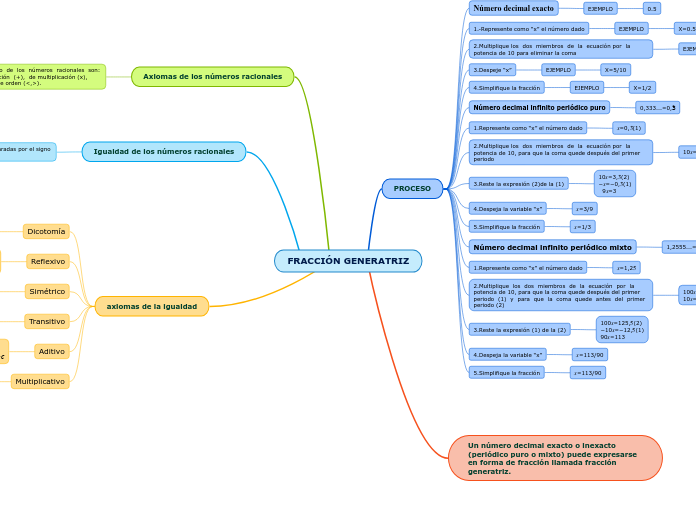
FRACCIÓN GENERATRIZ
av Joss Ivonne Lans för 4 årar sedan
1809

Mer av detta
4+2=6∧1/7=1/7⟶6/7=6/7
3+5=8∧3/2=3/2⟶19/2=19/2
3/6=1/2∧1/2=5/10⟶3/6=5/10
2/3=4/6⟷4/6<2/3
5/2=5/2
1/2=3/6
X=1/2
X=5/10
10X=5
X=0.5
0.5