av Demetrio Moschella för 2 årar sedan
295
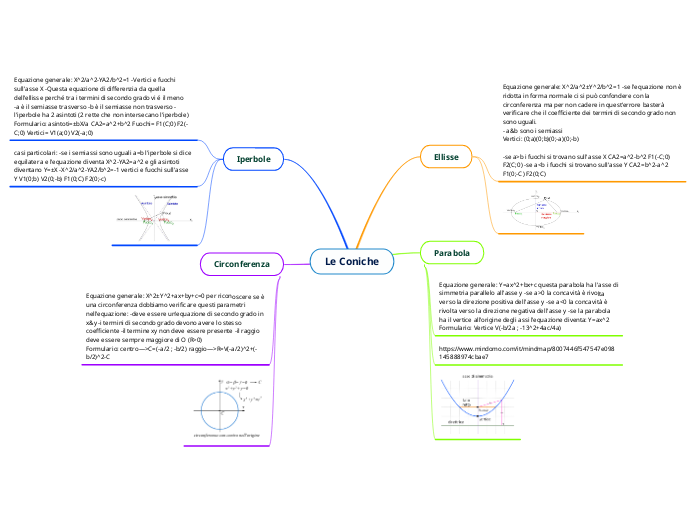
Le Coniche
Le coniche sono curve piane definite da equazioni algebriche di secondo grado in due variabili. Tra queste, l'iperbole è caratterizzata dall'avere due rami opposti e due asintoti, con un'
av Demetrio Moschella för 2 årar sedan
295

Mer av detta