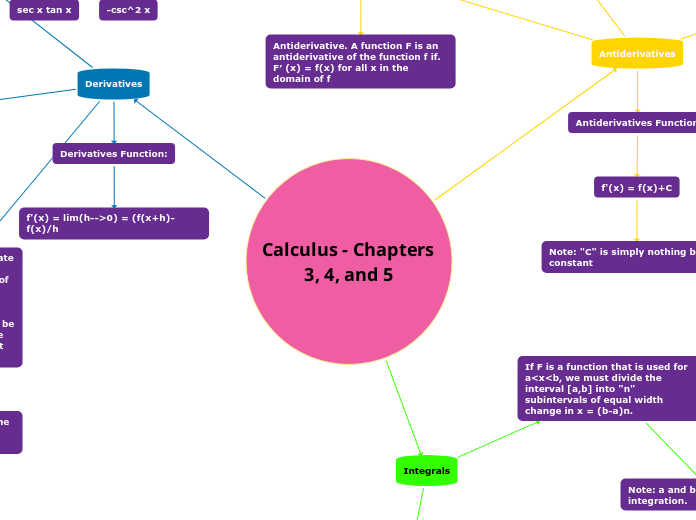
Calculus - Chapters 3, 4, and 5

It refers to the instantaneous rate of change of a quantity with respect to the pther. The slope of the tangent line to a curve at a particular point on the curve. Since a curve represents a function, its derivative can also be thought of as the rate of change of the corresponding function at the given point.

When you find the derivative, the value of x gets smaller and smaller.

Derivatives Function:

f'(x) = lim(h-->0) = (f(x+h)-f(x)/h

Trig Function

d/dx (sin x)

cos x

d/dx (cos x)

-sin x

d/dx (tan x)

sec^2 x

d/dx (csc x)

-csc x cot x

d/dx (sec x)

sec x tan x

d/dx (cot x)

-csc^2 x

Differentiation Rules

Sum rule

f'(x)=u'(x)+v'(x)

Difference rule

f'(x)=u'(x)-v'(x)

Chain rule

dy/dx = (dy/du) × (du/dx)

Quotient rule

f'(x) = (u'(x)*v(x)-u(x)*v'(x))/(v(x))^2

Product rule

f′(x) = u′(x) × v(x) + u(x) × v′(x)

A function F is an antiderivative of the function f if. F′ (x) = f(x) for all x in the domain of f

Antiderivative. A function F is an antiderivative of the function f if. F′ (x) = f(x) for all x in the domain of f

It's basically like you're solving a derivatives backwards

Let F be an antiderivative of f over an interval I. Then,
for each constant C, the function F(x)+C is also an antiderivative of f over I. If G is an antiderivative of f over I, there is a constant C for which G(x)=F(x)+C over I.

In other words, the most general form of the antiderivative of f over I is F(x)+C.

Antiderivatives Function

f'(x) = f(x)+C

Note: "C" is simply nothing but a constant

If F is a function that is used for a<x<b, we must divide the interval [a,b] into "n" subintervals of equal width change in x = (b-a)n.

Note: a and be are the limits of integration.

Definite Integral and Indefinite Integral

A definite integral is defined as the integral which has upper and lower limits and has a constant value as the solution

∫ab

Definite Integral properties:

∫ab f(x) dx = ∫ab f(t) d(t)
∫ab f(x) dx = – ∫ba f(x) dx
∫aa f(x) dx = 0
∫ab f(x) dx = ∫ac f(x) dx + ∫cb f(x) dx
∫ab f(x) dx = ∫ab f(a + b – x) dx
∫0a f(x) dx = f(a – x) dx

Function: ∫ab f(x) dx = F(b)-F(a)

An indefinite integral is defined as the internal which do not have limits applied to it and it gives a general solution for a problem

Function: ∫f(x) dx = F(x) + C

Indefinite Integral Properties:

∫ 1 dx = x + C
∫ a dx = ax + C
∫ xn dx = ((xn+1)/(n+1)) + C ; n ≠ 1
∫ sin x dx = – cos x + C
∫ cos x dx = sin x + C
∫ sec2x dx = tan x + C
∫ cosec2x dx = -cot x + C
∫ sec x tan x dx = sec x + C
∫ cosec x cot x dx = -cosec x + C
∫ (1/x) dx = ln |x| + C
∫ ex dx = ex + C
∫ ax dx = (ax/ln a) + C ; a > 0, a ≠ 1

∫