El poligono
Un polígono es el área de un plano que está delimitado por líneas que tienen que ser rectas.
Si hacemos caso a la etimología de la palabra, polígono proviene de los términos griegos «poli» y «gono«. «Poli» podría traducirse como «muchos» y «gono» como «ángulo». Atendiendo a esto podríamos decir que un polígono es literalmente aquello que tiene muchos ángulos.
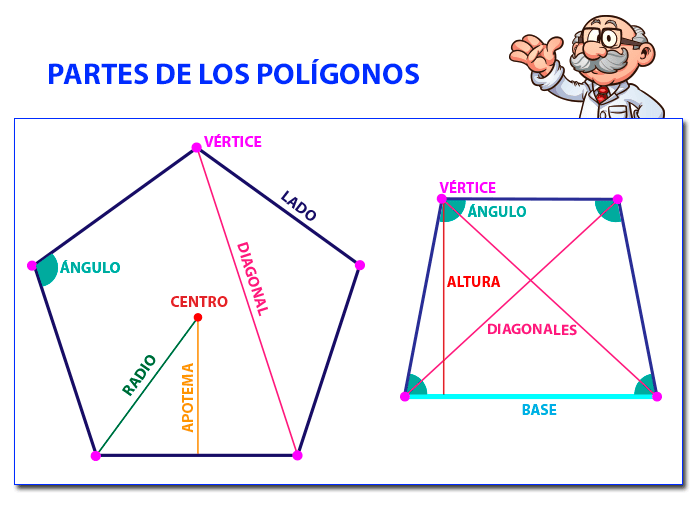
Partes de los polígonos: Lados: son los segmentos que forman la línea poligonal.
Vértices: son los puntos donde se unen los lados.
Ángulos: son las regiones del plano que delimitan dos lados.
Diagonal: es la recta que une dos vértices no consecutivos.
Centro: es el punto desde el que todos los ángulos y lados están a la misma distancia.
Radio: es el segmento que une el centro del polígono con cualquiera de sus vértices
Apotema: es el segmento que une el centro del polígono con el centro de cualquiera de sus lados.
Base: Es el lado inferior de un polígono. Normalmente es el lado donde se «apoya» la figura.
.Clasificación de polígonos
Podemos clasificar los polígonos de tres formas diferentes:
Clasificación de polígonos según sus lados:
Triángulo: 3 lados
Cuadrilátero: 4 lados
Pentágono: 5 lados
Hexágono: 6 lados
Heptágono: 7 lados
Octógono: 8 lados
Eneágono: 9 lados
Decágono: 10 lados
Endecágono: 11 lados
Dodecágono: 12 lados

Subtopic
.Clasificación de polígonos según sus ángulos:
Polígonos cóncavos: es cuando el polígono tiene un ángulo que mide más de 180º.
Polígonos convexos: es cuando todos los ángulos del polígono miden menos de 180º.
Subtopic
.Clasificación de polígonos según sus lados y sus ángulos:
Polígonos regulares: es cuando un polígono tiene todos sus lados y ángulos iguales.
Polígonos irregulares: es cuando en un polígono hay uno o más lados y/o ángulos que no son iguales.

Subtopic
Elementos del Polígono
Ángulos: los ángulos internos corresponden a los ángulos formados por dos lados consecutivos. Por otro lado, los ángulos externos son los ángulos formados por un lado y por la prolongación del lado sucesivo a él. Es importante resaltar que la suma de los ángulos externos de los polígonos es de 360º. Para obtener la suma de los ángulos internos de un polígono se utiliza la fórmula: S = (n-2).180, siendo n el número de lados.
Diagonal: corresponde al segmento de recta que une dos vértices no consecutivos, es decir, un segmento de recta que pasa por el interior de la figura. Para calcular el número de diagonales presentes en un polígono se utiliza la fórmula: d = n (n-3) / 2, donde n es el número de lados.
Lado: corresponde a cada segmento de recta que une vértices consecutivos..
Topic principal