HISTORIA DE SUCESIONES Y SERIES
EPOCAS
BALILONIOS (2000-600ac)
•Se cree que conocían la fórmula de interés compuesto y, por lo tanto, también las progresiones geométricas
•Se plantearon la pregunta ¿Cuánto tiempo se doblaría una cantidad de dinero a un determinado interés compuesto?

edad media
(1100-1400)
-Bhaskara II escribe su obra Lalavati, donde encuentra la solución a problemas de sucesiones aritméticas y geométricas
La sucesión de Fibonacci que tiene aplicaciones en fenómenos naturales (progresión relativa a una pareja de conejos)
Fibonacci escribe una obra sobre teoría de números, donde se estudian propiedades de números y series



Madhava de Sangamagramma obtuvo resultados que fueron redescubiertos por europeos tales como:
Serie infinita de la función arctang de Gregory (1668)
Serie de potencias de Newton para el seno (1700)
Serie de Maclaurin para el coseno (1700)
Serie para de Leibniz (1700)
Renacimiento
(1400-1600)
Se abordan y resuelven problemas relacionados con el algebra y las sucesiones
Nicolas de Cusa realiza escrito que se basan en la critica sobre la noción de infinito
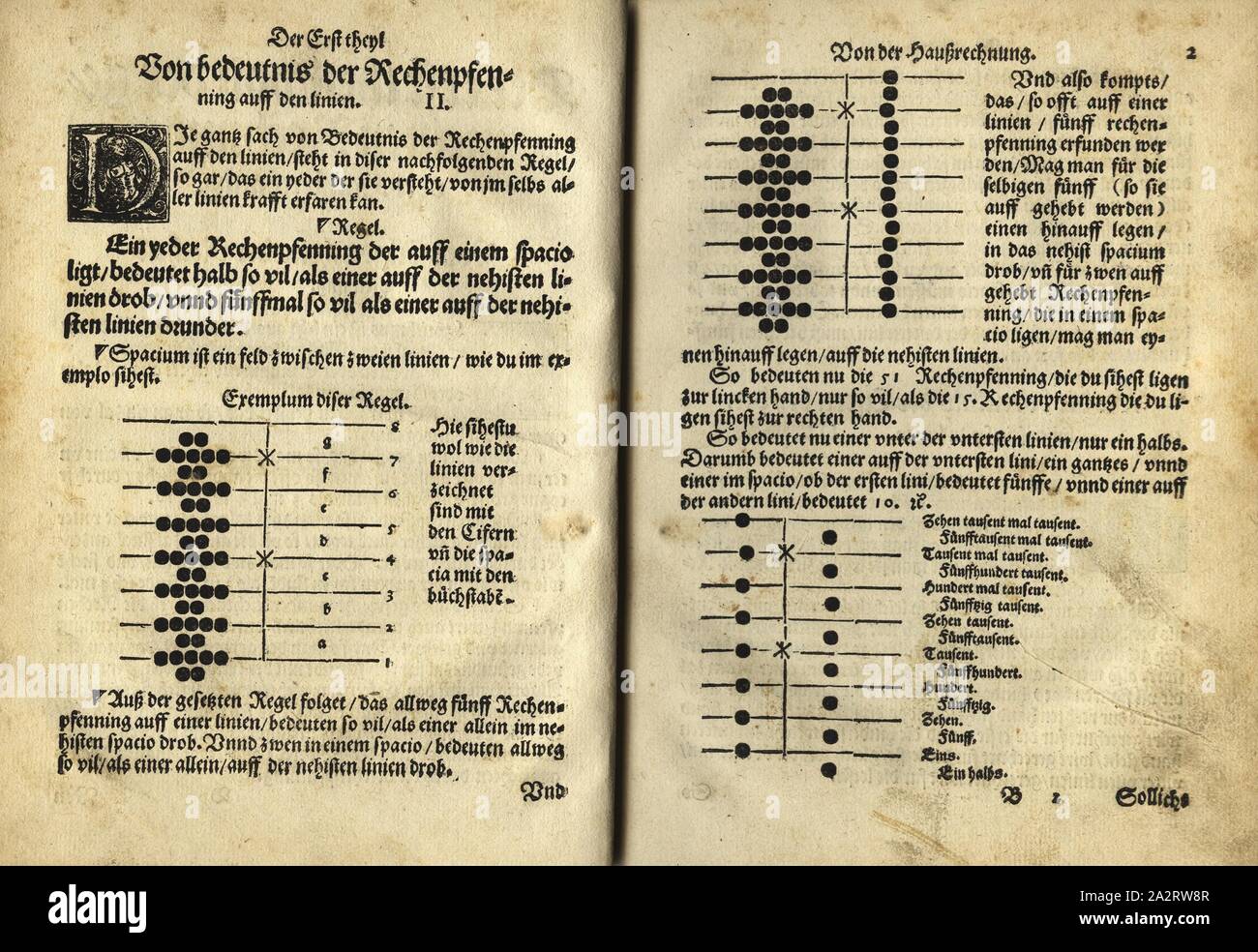
Michael Stifel realizó un estudio extenso sobre las series y progresiones aritméticas y geométricas


Edad contemporanea
(1600-actualidad)
Newton demuestra el Teorema del binomio Newton (desarrollo de potencias de sumandos como serie infinita de términos)
Leibnitz calcula π en forma de serie mediante la fórmula:

Heine, Philip Cantor y Karl Weierstrab realizan aportes al análisis mediante el estudio de los limites y el infinito

Walclav Sierpiski:
1916: Creó el fractal “la alfombra de Sierpiski”, que se basa en dividir un cuadrado en 3 partes iguales cada lado extrayéndolos del cuadrado central, repitiendo la operación con los nuevos cuadrados

1919: Creó el fractal “triángulo de Sierpiski” que se basa en tomar un triangulo equilátero, unir los puntos medios de los lados dejando un triangulo sombreado y repitiendo el proceso con dicho triangulo.

Louis Cauchy caracterizó el concepto de limite mediante las sucesiones e investigó la convergencia y divergencia de series y series de potencia
Gauss redescubrió como solucionar el problema de la suma de los 100 primeros números estableciendo una relación simétrica en esta progresión y contribuyó a la teoría de series de Euler
Otto Stolz estudió la convergencia de una sucesión a partir de una sucesión monótona creciente y divergente
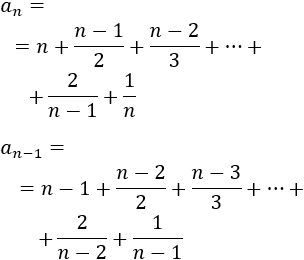

Fourier estableció la serie de Fourier que se basa en una función como serie de senos y cosenos
Leonhard Euler realizó aportes como
ANTIGUO EGIPTO
-El papiro Rhind: Conocimientos generales de series geométricas y aritméticas
-El papiro amhes: tablas de descomposición de 2/n y n/10 en suma de fracciones unitarias

ANTIGUA INDIA (500 AC-100 DC)
•Pingala en su obra expone ideas sobre los números de Fibonacci (llamados mātrāmeru)
•400ac-200ac: Matemáticos Yainas comienzan estudios de propósito matemático desarrollando sucesiones y progresiones
•El Manuscrito “Bakhshali”: Incluye soluciones de progresiones aritméticas, geométricas y series compuestas

ANTIGUA GRECIA (450 AC-300 DC)
-300ac uso de números figurales a causa del sistema de numeración de la época
-300 dc se empieza a hablar de sucesiones con números pares (ilimitado) e impares (limitado)
-Sucesiones mencionadas en la obra de Eudoxo (S. IV ac) y en la de Arquímedes (S. III ac)
-Ambos desarrollaron con éxito el método de exhausción. Está basado en la
propiedad arquimediana de los números y en la propiedad:
∀M ∈ R ∀r ∈[ 1/2 ,1 ) ⇒ lim n→∞ M ⋅〖(1- r)〗^(n )= 0}