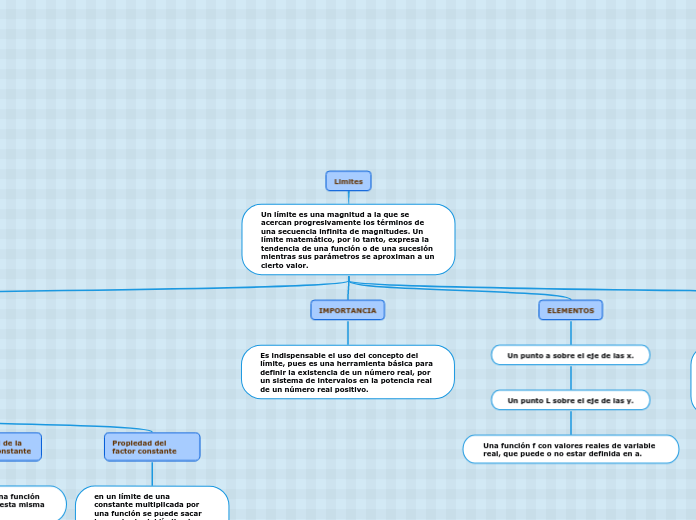
Limites
Un límite es una magnitud a la que se acercan progresivamente los términos de una secuencia infinita de magnitudes. Un límite matemático, por lo tanto, expresa la tendencia de una función o de una sucesión mientras sus parámetros se aproximan a un cierto valor.
PROPIEDADES DE LOS LÍMITES
Las propiedades de los límites son operaciones que se pueden emplear para simplificar el cálculo del límite de una función más compleja. Al tratarse de operaciones, también se le denimina álgebra de los límites.
Unicidad del límite
cuando el límite existe, el límite es único.
Fórmula de la unicidad de un límite
Propiedad del cociente
el límite de un cociente de dos funciones es el cociente de los límites de las mismas.
Propiedad de la suma
el límite de la suma es la suma de los límites.
Propiedad de la función potencial
el límite de una función potencial es la potencia del límite de la base elevado al exponente
Propiedad de la resta
el límite de la resta es la resta de los límites
Propiedad de la función exponencial
el límite de una función exponencial es la potencia de la base elevada al límite de la función exponente
Propiedad del producto
el límite del producto es el producto de los límites.
Propiedad de la función potencial exponencial
el límite de una función potencial exponencial, es la potencia de los límites de las dos funciones
Propiedad de la función constante
el límite de una función constante es esta misma constante.
Propiedad de la raíz
el límite de una raíz, es la raíz del límite
Propiedad del factor constante
en un límite de una constante multiplicada por una función se puede sacar la constante del límite sin que se afecte el resultado.
Propiedad de la función logarítmica
El límite del logaritmo es el logaritmo del límite.
IMPORTANCIA
Es indispensable el uso del concepto del límite, pues es una herramienta básica para definir la existencia de un número real, por un sistema de intervalos en la potencia real de un número real positivo.
ELEMENTOS
Un punto a sobre el eje de las x.
Un punto L sobre el eje de las y.
Una función f con valores reales de variable real, que puede o no estar definida en a.
TIPOS
LATERALES: si se habla de funciones, se entiende que es un estudio del comportamiento de la misma, en un punto específico. Pero si se aplica un análisis, por separado, entre los números menores al punto y mayores a él, se habla de límites laterales de una función.
INFINITOS: límite al infinito puede definirse como aquel al que tiende f(x) cuando la variable x se hace tan grande, tanto en positivo como en negativo, como queramos. Significa que la función f(x) puede tener un valor finito o puede ser infinita (límite infinito).
INDETERMINADOS: puede decirse que los límites indeterminados no indican que el límite no exista, más bien que no se puede anticipar el resultado. Es necesario hacer operaciones adicionales para eliminar la indeterminación y averiguar el valor del límite (en caso de que exista).