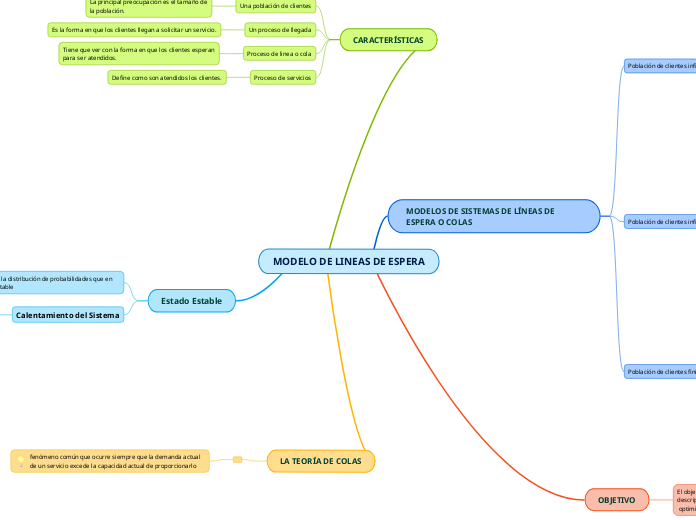
MODELO DE LINEAS DE ESPERA
MODELOS DE SISTEMAS DE LÍNEAS DE ESPERA O COLAS
Población de clientes infinita.
Clientes esperan en una sola fila y existe un solo
servidor
Probabilidad de Vacío (Po)
Probabilidad de Encontrar “n” Clientes en el Sistema (Pn)
Tiempo Promedio en el Sistema
Tiempo Promedio de Espera en Fila o Cola
Número Promedio de Clientes en el Sistema (Ls)
Número Promedio de Clientes en Fila o Cola (Lq)
Subtopic
Población de clientes infinita.
Clientes esperan en una sola fila y existen varios
servidores
Factor de Ocupación (δ)
Probabilidad de Vacío (Po)
Probabilidad de encontrar “n” clientes en el sistema (Pn)
Probabilidad de encontrar “n” clientes en el Sistema (Pn) Cuando n > K
Tiempo Promedio en el Sistema (Ws)
Tiempo Promedio de Espera en Fila o Cola (Wq)
Número Promedio de Clientes en el Sistema (Ls)
Número Promedio de Clientes en Fila o Cola (Lq)
Población de clientes finita.
clientes esperan en una sola fila y existe un solo
servidor
Probabilidad de Vacío (Po)
Probabilidad de Encontrar n Clientes en el Sistema (Pn) Cuando nK
Tiempo Promedio en el Sistema (Ws)
Tiempo Promedio de Espera en Fila o Cola (Wq)
Número Promedio de Clientes en el Sistema (Ls)
Número Promedio de Clientes en Fila o Cola (Lq)
OBJETIVO
El objetivo de los modelos de líneas de espera es más de descripción que de
optimización.
CARACTERÍSTICAS
Una población de clientes
La principal preocupación es el tamaño de
la población.
Un proceso de llegada
Es la forma en que los clientes llegan a solicitar un servicio.
Proceso de linea o cola
Tiene que ver con la forma en que los clientes esperan
para ser atendidos.
Proceso de servicios
Define como son atendidos los clientes.
Estado Estable
El estado estable es la distribución de probabilidades que en cierto punto será estable
Calentamiento del Sistema
Tiempo que requiere una simulación para alcanzar el estado estable, esté tiempo esta relacionado con la cantidad de actividades que ocurren en el sistema
LA TEORÍA DE COLAS
fenómeno común que ocurre siempre que la demanda actual de un servicio excede la capacidad actual de proporcionarlo