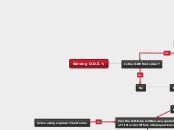
Is the O.D.E first order?
Can the O.D.E. be written as a system of first order differential equations?
Solution: y(t) = c1e^(λ1t)v1 + c2e^(λ2t)v2
Use the integrating factor method
Solution: calculate the integrating factor, multiply by the integrating factor, integrate, and solve for y. 1
Undetermined coefficients method
Complex (Imaginary) Roots
Solution: y(t) = e^(αt)[c1cos(βt) + c2sin(βt)] 1
Is the O.D.E. second order?
Solution: separate, integrate, and solve for y
Complex (Imaginary) Roots
Solution: y(t) = c1e^(αt)[cos(βt)p - sin(βt)q] + c2e^(αt)[sin(βt)p - cos(βt)q]
Solve using eigenvectors and eigenvalues if the O.D.E. can be written as a system of first order differential equations; otherwise, use laplace transforms.
Solution: y(t) = c1e^(r1t) + c2te^(r2t)
Solution for non-homogeneous: y(t) = (homogenous solution) + (particular solution)
Form the characteristic polynomial
Solve using laplace transforms
Solution: integrate and solve for y
Variations of parameters method
Use eigenvectors and eigenvalues
Can you integrate directly?
Solution: y(t) = c1e^(λt)v + c2te^(λt)v + c2e^(λt)u
Solution: y(t) = c1e^(r1t) + c2e^(r2t)
Find the homogeneous solution
Find the particular solution