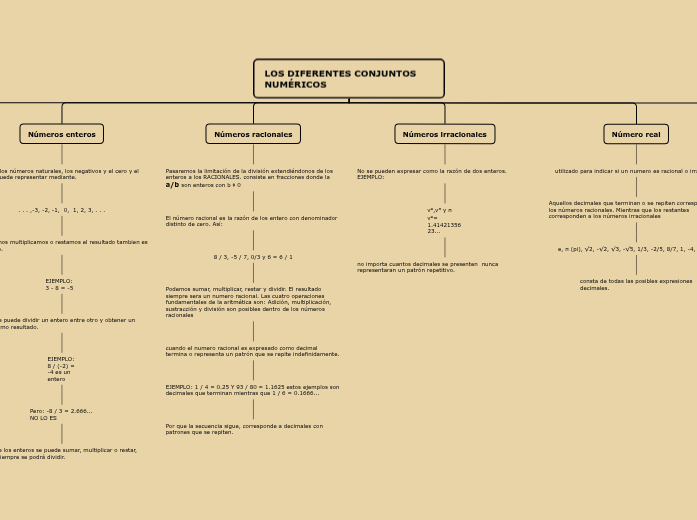
LOS DIFERENTES CONJUNTOS NUMÉRICOS

Al sumar o multiplicarlos números reales, el resultado siempre será un numero natural.

EJEMPLO: 4 + 6 = 10 Y 4 * 6 = 24

Al restar o dividir no siempre se obtiene un numero natural.

EJEMPLO: 7 - 10 = -3 Y 2 / 7 =0.28517...

Dentro de los números naturales se puede sumar multiplicar, pero no siempre podemos restar o dividir

Incluyen los números naturales, los negativos y el cero y el cero se puede representar mediante.

. . . ,-3, -2, -1, 0, 1, 2, 3, . . .

Si sumamos multiplicamos o restamos el resultado tambien es un entero.

EJEMPLO: 3 - 8 = -5

Aun no se puede dividir un entero entre otro y obtener un entero como resultado.

EJEMPLO:8 / (-2) = -4 es un entero

Pero: -8 / 3 = 2.666... NO LO ES

Dentro de los enteros se puede sumar, multiplicar o restar, pero no siempre se podrá dividir.

Pasaremos la limitación de la división extendiéndonos de los enteros a los RACIONALES. consiste en fracciones donde la a/b son enteros con b ǂ 0

El número racional es la razón de los entero con denominador distinto de cero. Así:

8 / 3, -5 / 7, 0/3 y 6 = 6 / 1

Podemos sumar, multiplicar, restar y dividir. El resultado siempre sera un numero racional. Las cuatro operaciones fundamentales de la aritmética son: Adición, multiplicación, sustracción y división son posibles dentro de los números racionales

cuando el numero racional es expresado como decimal termina o representa un patrón que se repite indefinidamente.

EJEMPLO: 1 / 4 = 0.25 Y 93 / 80 = 1.1625 estos ejemplos son decimales que terminan mientras que 1 / 6 = 0.1666...

Por que la secuencia sigue, corresponde a decimales con patrones que se repiten.

No se pueden expresar como la razón de dos enteros. EJEMPLO:

ѵ²,ѵ³ y π ѵ²= 1.4142135623...

no importa cuantos decimales se presenten nunca representaran un patrón repetitivo.

utilizado para indicar si un numero es racional o irracional.

Aquellos decimales que terminan o se repiten corresponden a los números racionales. Mientras que los restantes corresponden a los números irracionales

e, π (pi), √2, -√2, √3, -√5, 1/3, -2/5, 8/7, 1, -4, 0, 5...

consta de todas las posibles expresiones
decimales.

los números positivos se representan por los puntos a la derecha del cero y los números negativos a la izquierda de cero.

si A es un punto a la derecha de cero tal que OA tienen longitud unitaria A representa al numero uno.

Los enteros 2, 3, . . . n, . . . Estan representados por los puntos A2, A3, . . .An, . . .Estan a la derecha de cero y son tales que OA2 = 2OA, OA3=3OA, . . .OAn = nOA

En esta forma todos os enteros pueden representarse mediante puntos sobre la recta númerica.