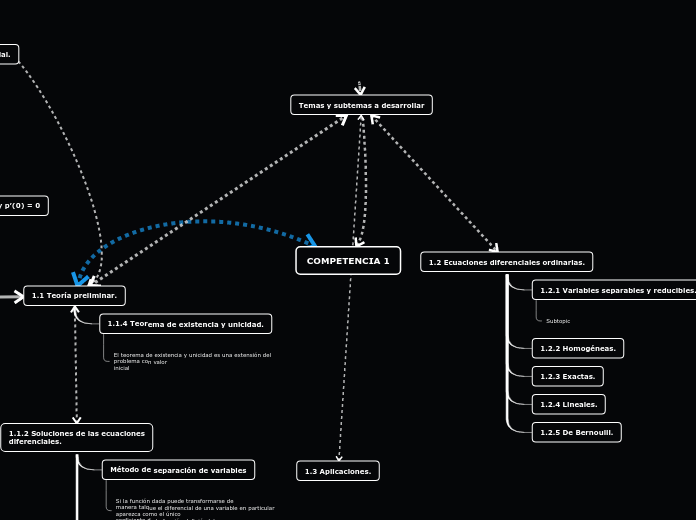
COMPETENCIA 1
1.1 Teoría preliminar.
1.1.4 Teorema de existencia y unicidad.
El teorema de existencia y unicidad es una extensión del problema con valor
inicial
1.1.1 Definiciones (Ecuación
diferencial, orden, grado, linealidad)
Como su nombre lo indica, una ecuación diferencial es aquella ecuación que contiene
algunos términos diferenciales. Estos son los diferenciales de la función que contiene
la variable dependiente de la ecuación diferencial dada. Contiene también una o
varias variables independientes.
Orden de una ecuación diferencial
d2y/ dx2 – 2yx2 = 9x
Grado de una ecuación diferencial
d2y/ dx2 – 2yx2 = 9x
Ecuación diferencial lineal
(x^{(n)},...,x',x,t)=0}
Ecuación diferencial no lineal
Ecuación diferencial Cuasi lineal
f1(z)=az+b}.
1.1.2 Soluciones de las ecuaciones
diferenciales.
Método de separación de variables
Si la función dada puede transformarse de
manera talque el diferencial de una variable en particular aparezca como el único
coeficiente de la función definiéndola
2. Ecuación diferencial homogénea
En el caso que la
técnica anterior no funcione, entonces comprueba la homogeneidad de la
ecuación
1.1.3 Problema de valor inicial.
Las ecuaciones diferenciales pueden ser de dos tipos principalmente, una
ecuación diferencial ordinaria y una ecuación diferencial parcial. También
sabemos que una ecuación diferencial se compone del derivado de una función
indefinida, la función indefinida y una variable autónoma.
p+ p – 6p = 0 dado que p(0) = 5 y p’(0) = 0
Temas y subtemas a desarrollar
1.2 Ecuaciones diferenciales ordinarias.
1.2.1 Variables separables y reducibles.
Subtopic