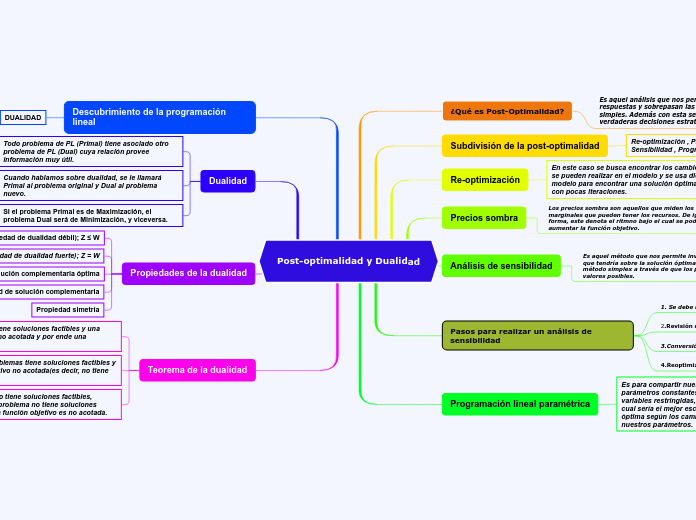
Post-optimalidad y Dualidad
¿Qué es Post-Optimalidad?
Es aquel análisis que nos permite responder o dar respuestas y sobrepasan las soluciones óptimas simples. Además con esta se pueden tomar verdaderas decisiones estratégicas.
Subdivisión de la post-optimalidad
Re-optimización , Precios Sombra, Análisis de Sensibilidad , Programación lineal paramétrica
Re-optimización
En este caso se busca encontrar los cambios que se pueden realizar en el modelo y se usa dicho modelo para encontrar una solución óptima nueva y con pocas iteraciones.
Precios sombra
Los precios sombra son aquellos que miden los valores marginales que pueden tener los recursos. De igual forma, este denota el ritmno bajo el cual se podra aumentar la función objetivo.
Análisis de sensibilidad
Es aquel método que nos permite investigar el efecto que tendría sobre la solución óptima que proporciona el método simplex a través de que los parámetros tengan valores posibles.
Muestra: solución es sensibles a cambios y que requieren exactitud al momento de calcularlos y monitoreo constante durante la implementación de la solución.
Parámetros sensibles: Son aquellos valores que se pueden cambiar sin que cambien la solución óptima.
Pasos para realizar un análisis de sensibilidad
1. Se debe revisar el modelo.
2.Revisión de la table de Símplex
3.Conversión apropiada de eliminación de Gauss
4.Reoptimización
Programación lineal paramétrica
Es para compartir nuestra solución óptima en parámetros constantes y nuestros parámetros en variables restringidas, de manera que podemos ver cual sería el mejor escenario para nuestra solución óptima según los cambios que podemos hacer a nuestros parámetros.
Descubrimiento de la programación lineal
DUALIDAD
Dualidad
Todo problema de PL (Primal) tiene asociado otro problema de PL (Dual) cuya relación provee información muy útil.
Cuando hablamos sobre dualidad, se le llamará Primal al problema original y Dual al problema nuevo.
Si el problema Primal es de Maximización, el problema Dual será de Minimización, y viceversa.
Propiedades de la dualidad
Propiedad de dualidad débil); Z ≤ W
Propiedad de dualidad fuerte); Z = Wundefined
Propiedad de solución complementaria óptima
Propiedad de solución complementaria
Propiedad simetría
Teorema de la dualidad
Si un problema tiene soluciones factibles y una función objetiva no acotada y por ende una solución óptima.
Si uno de los problemas tiene soluciones factibles y una función objetivo no acotada(es decir, no tiene solución óptima).
Si un problema no tiene soluciones factibles, entonces el otro problema no tiene soluciones factibles o bien la función objetivo es no acotada.undefined