SECCIONES CÓNICAS
¿Cuáles son las secciones cónicas?
CIRCUNFERENCIA
La circunferencia es una figura geométrica cuyos puntos están a una distancia constante, llamada radio (r), del centro (C).
ELEMENTOS
Centro, el punto interior equidistante de todos los puntos de la circunferencia
Radio, el segmento que une el centro con un punto cualquiera de la circunferencia,
FÓRMULAS

GRÁFICO
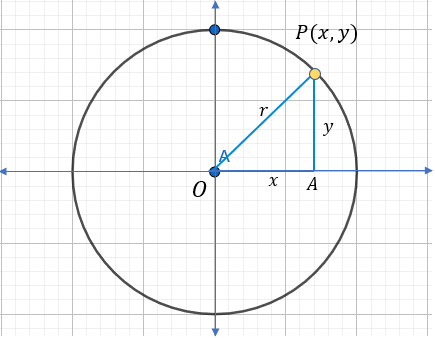
Con centro en (0,0)undefined
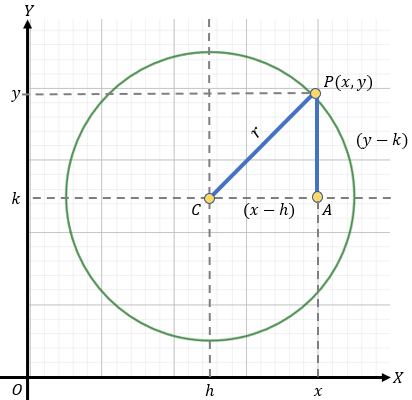
Con centro en (h,k)undefined
PARÁBOLAundefined
La parábola es el lugar geométrico de los puntos que equidistan del foco (F) y de una recta denominada directriz.
ELEMENTOS
1. Foco: Es el punto fijo F.
2. Directriz: Es la recta fija d.
3. Parámetro: Es la distancia del foco a la directriz, se designa por la letra p.
4. Eje: Es la recta perpendicular a la directriz que pasa por el foco.
5. Vértice: Es el punto de intersección de la parábola con su eje.
6. Radio vector: Es un segmento que une un punto cualquiera de la parábola con el foco.
FÓRMULAS

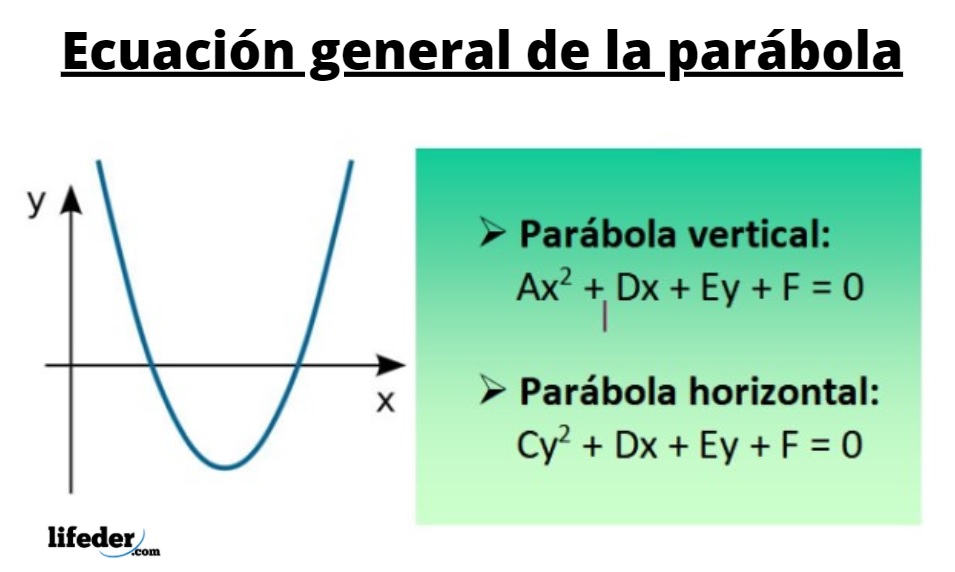
GRÁFICO
ELIPSEundefined
La elipse es el lugar geométrico de los puntos del plano cuya suma de las distancias a los dos focos (puntos interiores fijos F1 y F2) es constante. Es decir, para todo punto a de la elipse, la suma de las distancias d1 y d2 es constante.
ELEMENTOS
1. Focos: Son los puntos fijos F y F'.
2. Eje focal: Es la recta que pasa por los focos.
3. Eje secundario: Es la mediatriz del segmento FF'.
4. Centro: Es el punto de intersección de los ejes.
5. Distancia focal: Es el segmento de longitud 2c, c es el valor de la semidistancia focal.
6. Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
7. Centro de simetría: Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.
FÓRMULAS



GRÁFICO
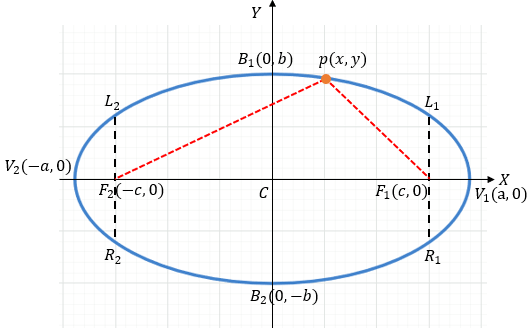
Con centro en (0,0) horizontalundefined
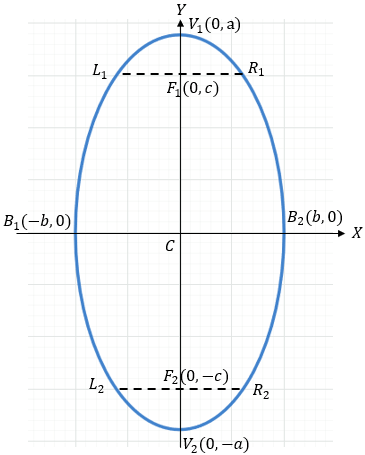
Con centro en (0,0) vertical
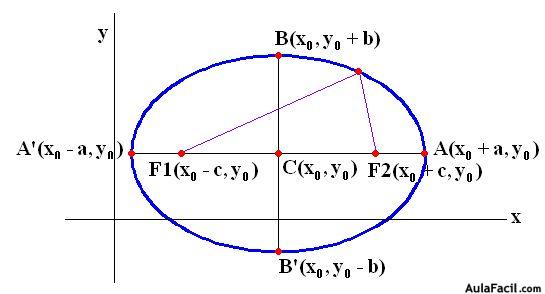
Con centro en (h,k) horizontal
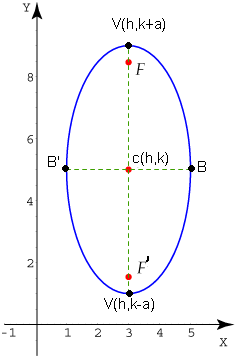
Con centro en (h,k) vertical
HIPÉRBOLAundefined
La hipérbola es el lugar geométrico de los puntos de un plano cuya diferencia de distancias (d1 y d2) a dos puntos fijos llamados focos (F1 y F2) es constante.
ELEMENTOS
1. Focos: Son los puntos fijos F y F'.
2. 2Eje focal, principal o real: Es la recta que pasa por los focos.
3.Centro: Es el punto de intersección de los ejes.
4. Vértices: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal.
5. Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'.
6. Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.
FÓRMULAS



GRÁFICO
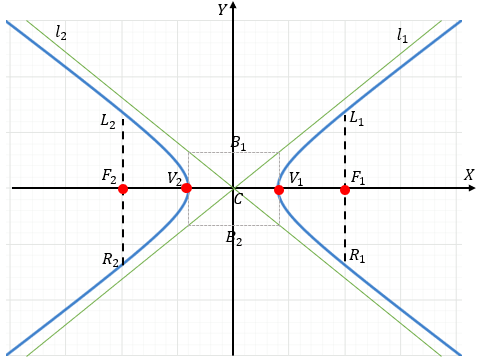
Con centro en (0,0)undefined
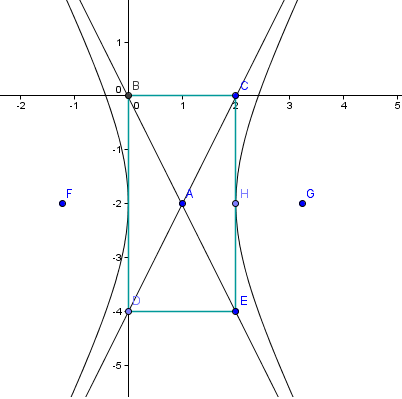
Con centro en (h,k)
El matemático griego Menecmo (vivió sobre el 350 A.C.) descubrió estas curvas y fue el matemático griego Apolonio (262-190 A.C.) de Perga (antigua ciudad del Asia Menor) el primero en estudiar detalladamente las curvas cónicas y encontrar la propiedad plana que las definía.Apolonio descubrió que las cónicas se podían clasificar en tres tipos a los que dio el nombre de: elipses, hipérbolas y parábolas.
Existen cuatro tipos de cónicas, según el ángulo del plano que intersecta con el cono y su base:
1. Circunferencia: es la intersección del cono con un plano paralelo a la base.
2. Elipse: intersección del cono con un plano oblicuo a la base y que no la corta en ningún momento.
3. Parábola: es la intersección del cono con un plano paralelo a su generatriz y que corta a la base.
4. Hipérbola: es la intersección de un cono recto y un plano cuyo ángulo es menor al de la generatriz del cono.