superficies en el espacio
hay tres tipos de superficie en el espacio que son
superficies de revolución
Una superficie de revolución es aquella que se genera mediante la rotación de una curva plana, o generatriz, alrededor de una recta directriz, llamada eje de rotación, la cual se halla en el mismo plano que la curva.
Ejemplos comunes de una superficie de revolución son:
Superficie de revolución.
Una superficie de revolución cilíndrica es generada por la rotación de una línea recta, paralela al eje de rotación, alrededor del mismo; esta superficie determina un volumen denominado cilindro, que se denomina sólido de revolución; la distancia entre el eje y la recta se denomina radio.
Una superficie de revolución cónica es generada por la rotación de una recta alrededor de un eje al cual interseca en un punto.
superficies cilíndricas
La superficie cilíndrica está conformada por rectas paralelas, denominadas generatrices, las cuales contienen los puntos de una curva plana, denominada directriz del cilindro. La superficie lateral cilíndrica se obtiene mediante el giro de una recta alrededor de un eje.
formula
Las superficies cilíndricas pueden ser
*superficie cilíndrica de revolución: si todas las generatrices equidistan de un eje, paralelo a ella.
*superficie cilíndrica de no revolución: si no existe un eje que equidiste de las generatrices.
Las superficies en el espacio es un concepto intuitivo. Hace referencia a objetivos que tienen área pero no volumen.

tenemos seis superficies CUADRICAS
HIPERBOLOIDE
Es el cuerpo engendrado por una elipse que se mueve de forma paralela y semejante a
sí misma, apoyando continuamente los extremos de sus ejes sobre las dos ramas de una
hipérbola.
formula

ejercicio
Si la elipse del cuerpo anterior se apoya únicamente en la parte interior de una rama
de la hipérbola y posteriormente en la otra, entonces resulta el hiperboloide de dos hojas.
formula
ejercicio
CONO ELIPTICO
Un cono elíptico es el cuerpo engendrado por una recta que, pasando continuamente
por un punto O, se apoya sobre dos elipses paralelas e iguales situadas simétricamente
respecto de un plano que contiene al punto citado. El cono, por consiguiente, está constituido por dos superficies iguales dispuestas de
forma especular respecto de un plano que pasa por el punto O (vértice del cono).
formula
EJERCICIO
PARABOLOIDE
ELIPTICO
El paraboloide, análogamente a la parábola en las secciones cónicas, es una superficie
sin centro que, en el caso general de ser elíptico, se define como:
Aquella superficie que engendra una elipse variable al moverse de forma perpendicular
sobre el eje de una parábola, de forma que mantiene constantemente los vértices de uno de sus
ejes sobre dicha curva
formula

ejercicio

HIPERBOLICO
Es la superficie engendrada por una hipérbola que, conservándose semejante a sí
misma, se mueve a lo largo de una parábola directora. También puede definirse como la
superficie generada por una parábola que, conservándose semejante a sí misma, se mueve a lo
largo de una de las ramas de una hipérbola directora.
formula
ejercicio
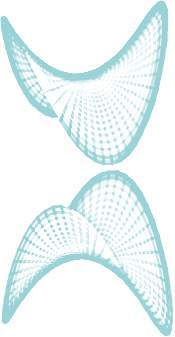
ELIPSOIDE
Un elipsoide es la superficie engendrada por una elipse de semiejes variables a y b que
se mueve perpendicularmente al eje 2c de una segunda elipse, de forma que los extremos del eje
2a se apoyan continuamente sobre la segunda elipse, y el eje 2b varía según una relación de
semejanza establecida respecto del eje 2a.
formula

Ejercicio