Triángulos

clasificación
elementos secundarios de un triángulo

altura
ortocentro . donde se intersectan las alturas

Add your text

bisectriz

Add your text

Add your text
Incentro: punto de intersección de las bisectrices

Transversal de Gravedad
SI CD: transversal de gravedad. AD=DB=CD. Y el ángulo ACB = 90°

El centro de gravedad divide a cada transversal en la razón 2:1
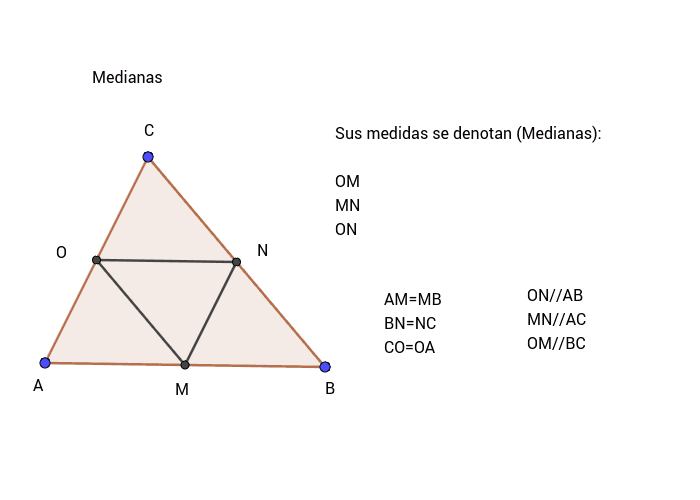
MEDIANA
Los triángulos que se forman son congruentes.
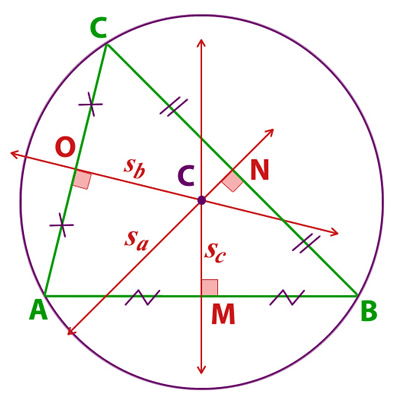
simetral
CA = CB = CC = radio de la circunferencia circunscrita al triangulo ABC.
Es la recta perpendicular que pasa por
el punto medio de cada lado del triángulo. Cada
mediana es paralela al lado opuesto y mide la
mitad de dicho lado.
Geometria Proporcional. En triángulos
criterios de congruencia

Criterio ALA (Ángulo-Lado-Ángulo):

Criterio LLL (Lado-Lado-Lado)

Criterio LLA (Lado-Lado-Ángulo Mayor):

Criterio LAL (Lado – Ángulo – Lado):
Triangulos semejantes

Ángulo – Ángulo (AA):
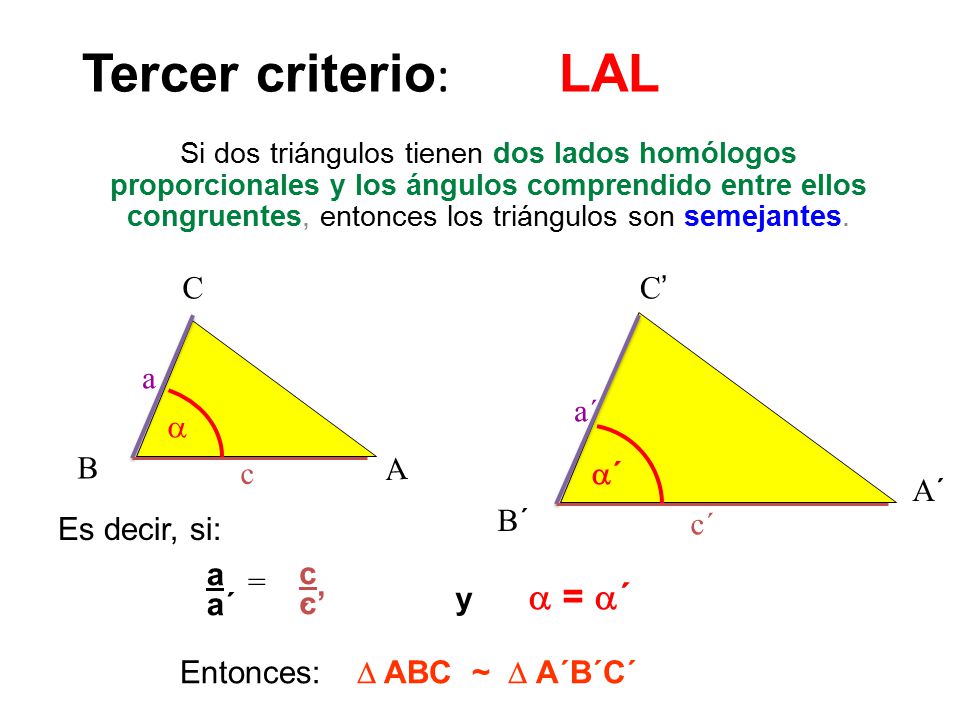
Lado Proporcional-Ángulo-Lado Proporcional
(LAL):

Lado Proporcional – Lado P. – Lado P. (LLL):
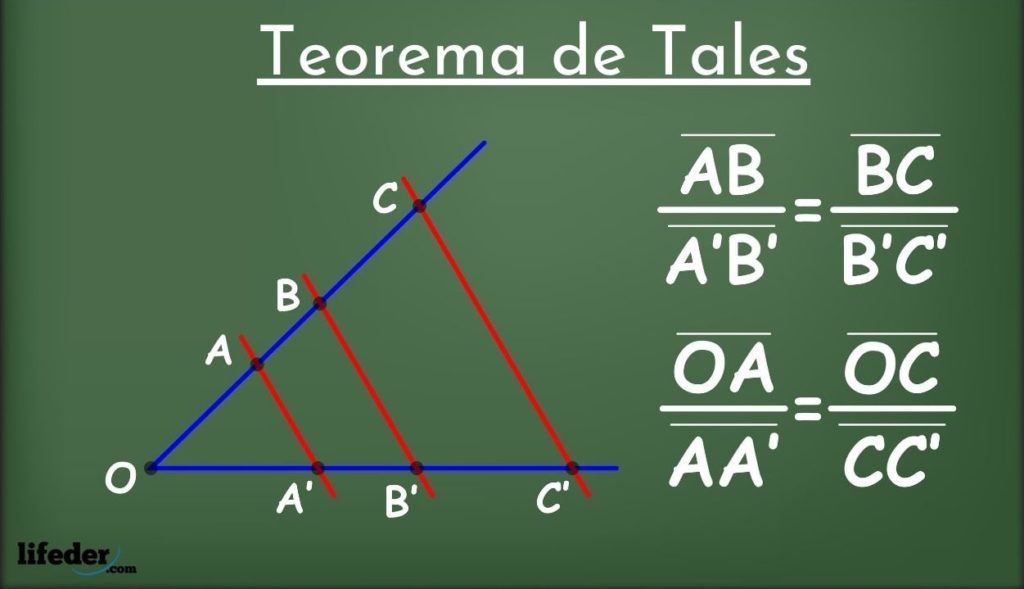
Teorema de Thales:

Add your text

Add your text

Teorema de Apolonio:
Triángulo Rectángulo
areas y perímetro
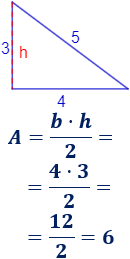
area
teoremas
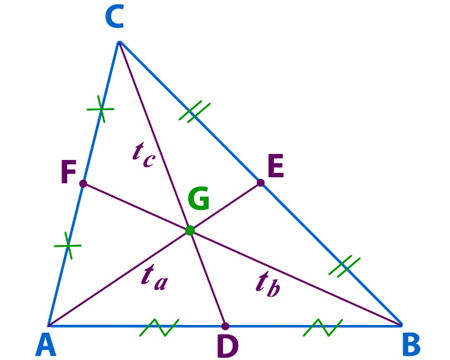
Teorema Transversal de Gravedad y Triángulo
Rectángulo:

Add your text
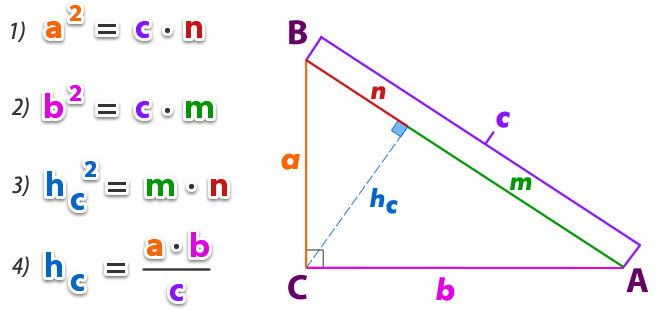
Teorema de Euclides

triángulo equilatero
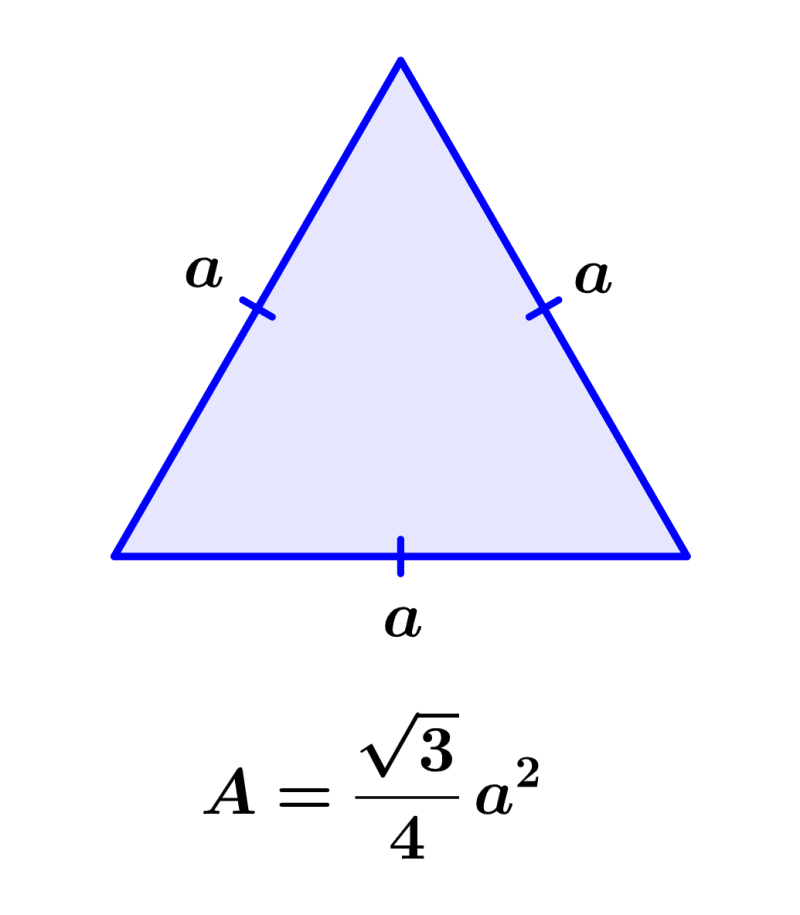
área

Add your text
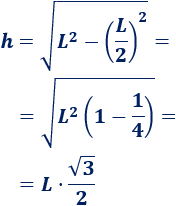
Add your text
teoremas relativos al tríangulo isóceles
Teorema 1: En todo triángulo isósceles coinciden
los elementos secundarios correspondientes al
lado distinto.
bisectrices=alturas=simetrales
Add your text