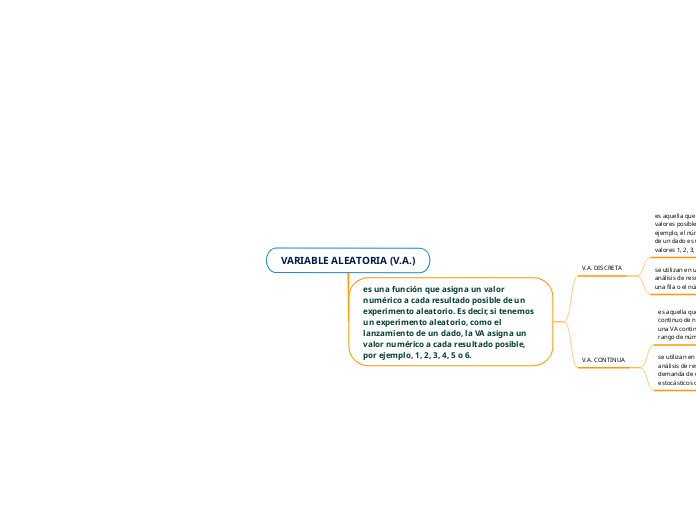
VARIABLE ALEATORIA (V.A.)

es una función que asigna un valor numérico a cada resultado posible de un experimento aleatorio. Es decir, si tenemos un experimento aleatorio, como el lanzamiento de un dado, la VA asigna un valor numérico a cada resultado posible, por ejemplo, 1, 2, 3, 4, 5 o 6.

V.A. DISCRETA

es aquella que puede tomar un conjunto finito o numerable de valores posibles, es decir, valores aislados o separados. Por ejemplo, el número de caras que aparece en el lanzamiento de un dado es una VA discreta, ya que solo puede tomar los valores 1, 2, 3, 4, 5 o 6.

se utilizan en una amplia variedad de aplicaciones, como el análisis de resultados de encuestas, el conteo de personas en una fila o el número de errores en una tarea repetitiva.

V.A. CONTINUA

es aquella que puede tomar cualquier valor en un rango continuo de números. Por ejemplo, la altura de las personas es una VA continua, ya que puede tomar cualquier valor en el rango de números entre 0 y un valor máximo posible.

se utilizan en una amplia variedad de aplicaciones, como el análisis de resultados de medición física, la predicción de la demanda de un producto o la simulación de procesos estocásticos complejos.

es un valor numérico que representa el valor esperado de la VA en un experimento aleatorio. La esperanza se calcula como la suma ponderada de los valores posibles de la VA, donde la ponderación es la probabilidad de que la VA tome cada valor posible.

La esperanza de una VA discreta se denota por E(X) y se define como:

E(X) = Σx * p(x) se utiliza para caracterizar la posición central de la distribución y es una medida de tendencia central. Por ejemplo, si la VA representa el número de puntos obtenidos en un lanzamiento de dado, la esperanza se puede utilizar para predecir el número esperado de puntos en varios lanzamientos.

es una medida de dispersión que indica cuánto se desvían los valores de la VA respecto a su esperanza. La varianza se calcula como la suma ponderada de las desviaciones cuadráticas de la VA respecto a su esperanza, donde la ponderación es la probabilidad de que la VA tome cada valor posible.

La varianza de una VA discreta se denota por Var(X) o σ² y se define como:

Var(X) = E((X - E(X))²) = Σ(x - E(X))² * p(x) se utiliza para caracterizar la dispersión de la distribución y es una medida de tendencia de la VA Por ejemplo, si la VA representa la cantidad de tiempo que tarda un proceso en completarse, la varianza se puede utilizar para predecir la necesita en el tiempo de procesamiento.

FUNCION DE PROBABILIDAD DE UNA VA DISCRETA

es una función matemática que indica la probabilidad de que la VA tome cada uno de los valores posibles. Esta función se define como:
P(X = x) = p(x)

se utiliza para calcular la probabilidad de eventos o conjuntos de eventos que involucren la variable aleatoria. Por ejemplo, si la variable aleatoria representa el número de caras que aparece en el lanzamiento de dos dados, la función de probabilidad se puede utilizar para calcular la probabilidad de que el número de caras sea mayor que 3 o menor que 5.

UNCIÓN DE DISTRIBUCIÓN DE UNA VA DISCRETA

es una función matemática que indica la probabilidad acumulada de que la VA tome un valor menor o igual que un valor dado. La función de distribución se define como:
F(x) = P(X ≤ x) La función de distribución de una VA discreta se construye sumando las probabilidades de cada valor posible de la VA hasta el valor x, es decir:
F(x) = P(X ≤ x) = Σp(i)

se utiliza para calcular la probabilidad de eventos o conjuntos de eventos que involucren la variable aleatoria. Además, se puede utilizar para calcular medidas de tendencia central y dispersión de la VA discreta, como la media y la varianza.

VARIACIÓN DE UNA VA DISCRETA

ESPERANZA DE UNA VA DISCRETA