Лента времени основных событий жизни Леонарда Эйлера
Аудиозапись - Немного об Эйлере
О Чебышеве писали
Шарль Эрмит
"Гордость науки России, один из первых математиков Европы, один из величайших математиков всех времён."
А.А.Марков
"Труды Чебышёва носят отпечаток гениальности. Он изобрёл новые методы для решения многих трудных вопросов, которые были поставлены давно и оставались нерешёнными. Вместе с тем он поставил ряд новых вопросов, над разработкой которых трудился до конца своих дней."
Помощники Эйлера
В последние годы жизни ученый продолжал усердно работать, пользуясь для чтения "глазами старшего сына" и ряда своих учеников
Н.И.Фусс
В 1772 г. Леонард Эйлер, ослепший на оба глаза и испытывающий из-за этого большие затруднения в работе, обратился с просьбой к своему земляку и другу - математику Даниилу Бернулли, чтобы он подыскал для него постоянного помощника из числа своих учеников, способного помогать ему в обширных вычислениях, а также быть его секретарем. По рекомендации Д. Бернулли, в 1772 г. 17-летний Н. Фусс отправился в Санкт-Петербург, где впоследствии прожил 10 лет в семье Л. Эйлера. Н. Фусс вёл переписку Л. Эйлера, делал вычисления по его указаниям, читал вслух математические сочинения, подготавливал статьи к печати, представлял его работы на заседаниях Академического собрания (более 160 работ) и всячески помогал в работе.
М.Головин
Михаил Евсеевич Головин - племянник Ломоносова. Его учителем был великий математик и физик Леонард Эйлер, работавший в то время в Петербургской Академии наук и деятельно участвовавший в подготовке русских математиков. Михаил Головин оказывал большую помощь своему учителю, терявшему в конце жизни зрение, в подготовке к изданию трудов по математике, механике и физике, участвовал в разработке ряда теоретических вопросов, интересовавших Л. Эйлера.
А.Лексель
Русский астроном А. И. Лексель, часто помогал слепому ученому в оформлении его работ по астрономии.
Потомки Эйлера
Из 13 детей Эйлера лишь пять преодолели младенческий возраст. Из трех его сыновей старший Иоганн-Альбрехт также стал действительным членом Академии, многие годы был непременным секретарем её, в последние годы жизни отца выступал в некоторых работах его соавтором. Средний стал врачом, младший - военным. Две дочери хотя и оставили потомков, но не пережили отца, У Эйлера было 45 внуков, к концу его жизни в живых оставалось - 26. Десятки и даже сотни потомков Эйлера, в том числе прямых, с сохранением родовой фамилии, живут в России и других странах. (Результаты огромной работы по составлению этого родословного древа (прослеженного до XIII века), проделанной двумя его отдаленными потомками в середине ХХ века, были опубликованы в 1988г. в юбилейном сборнике к 275-летию Л. Эйлера
Герб Эйлеров
Сказка о дружественных числах
Математические объекты носящие имя Леонарда Эйлера
- теорема Эйлера в теории чисел
- теорема вращения Эйлера
- теорема Эйлера в планиметрии
- теорема Эйлера в комбинаторике
- гипотеза Эйлера в теории чисел
- теорема Эйлера для многогранников
- лемма Эйлера
- уравнения Эйлера – Лагранжа
- уравнения Эйлера – Пуассона
- уравнения Эйлера в механике
- уравнение Эйлера в гидродинамике
- эйлеровы точки либрации
- уравнение Эйлера – Бернулли
- функция Эйлера в теории чисел
- функция Эйлера в комплексном анализе
- тождество Эйлера в теории чисел
- тождество Эйлера в комплексном анализе
- тождество Эйлера о четырёх квадратах
- тождество Эйлера в алгебре многочленов
- формула Эйлера в комплексном анализе
- формула Эйлера в кинематике твёрдого тела
- формула Эйлера в геометрии треугольника
- формула Эйлера в геометрии четырёхугольника
- формула Эйлера для суммы первых членов гармоничного ряда.
- формула Эйлера в теории графов
- эйлерова характеристика (алгебраическая топология)
- интегралы Эйлера первого рода и второго рода
- интеграл Эйлера – Пуассона
- постоянная Эйлера – Маскерони
- число Эйлера
- углы Эйлера
- многочлены Эйлера
- преобразование Эйлера
- прямая Эйлера в геометрии треугольника
- окружность Эйлера (окружность девяти точек)
- круги Эйлера
- эйлеров цикл, эйлерова цепь, эйлеров граф в теории графов
- эйлеров сплайн
- эйлерова сила
Второй Ломоносов России 18 столетия
В том усомниться
Мог ли кто-то,
Что Эйлер удивит весь мир,
Что только цифры и расчёты
Его единственный кумир.
Леонард Эйлер занимался поиском дружественных чисел.
Он получил утверждение, очень похожее на правило Сабита, но более общее. Правда, с помощью своего обобщения он не смог найти новые дружественные числа, так как в то время необходимые ему таблицы простых чисел были составлены только до 100 000.
Эйлер искал дружественные числа и совершенно иного вида, чем его предшественники, в частности нечетные. Среди его «трофеев» оказались и пары нечетных дружественных чисел вида
а · p · q и а · r где р, q, r – простые числа. Например:
(32 · 7 · 13) · 5 · 17 и (32 · 7 · 13) · 107;
(34 · 5 · 11) · 29 · 89 и (34 · 5 · 11) · 2699.
В своих мемуарах «О дружественных числах» и «О сумме делителей» Эйлер излагает пять различных методов выявления дружественных чисел. Математик нашёл 59 пар дружественных чисел. И это в короткий период – с 1747 года по 1750 год!
Общие интересы к теории чисел
Х.Гольдбах
Писали об Эйлере
С.И.Вавилов
"Вместе с Петром I и Ломоносовым, Эйлер стал добрым гением нашей Академии, определившим её славу, её крепость, её продуктивность".
Современник Эйлера
"Математические формулы у Эйлера жили своей собственной жизнью и рассказывали ему важные и существенные данные о природе вещей. Ему было достаточно только коснуться их, как они из немых букв преображались в красноречивые фразы, дающие глубокий и значительный ответ на различные вопросы".
Доминик Араго
"Эйлер вычислял без всякого видимого усилия, как человек дышит или как орёл парит над землёй".
Названы в честь Эйлера
5.Золотая медаль им. Эйлера РАН
4.Институт им. Эйлера РАН в Петербурге
3.Улица в Алма-Ате
2.Астероид
1.Кратер на луне
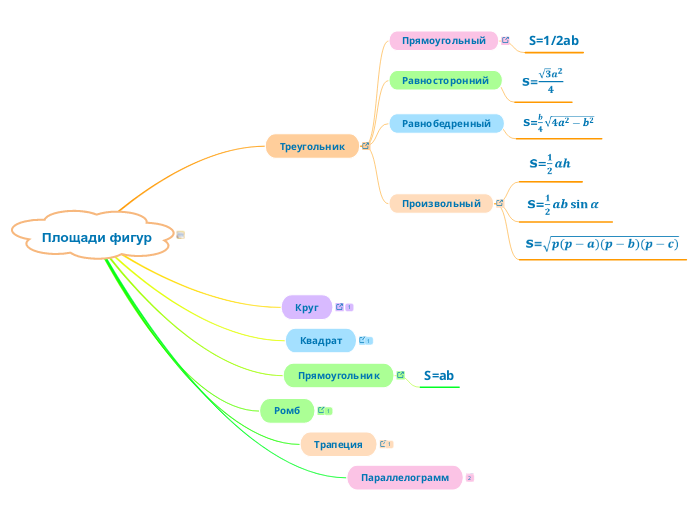
Определение дружественных чисел
Дружественные числа — два различных натуральных числа, для которых сумма всех собственных делителей первого числа равна второму числу и наоборот, сумма всех собственных делителей второго числа равна первому числу.
Поиск продолжается
На сентябрь 2007 года было известно 11 994 387 пар дружественных чисел. Все они состоят из чисел одной чётности. 30 января 2017 года запущен проект распределённых вычислений на платформе BOINC — Amicable Numbers. Поиск дружественных чисел осуществляется как с помощью расчётов на процессоре так и на видеокарте.
Найдите свою половинку с помощью дружественных чисел!
Первую пару чисел 220 и 284 в древности считали символом дружбы. Мартин Гарднер в книге «Математические новеллы» рассказывает о том, что в Средние века были распространенные талисманы с выгравированными на них числами 220 и 284, якобы способствующими укреплению любви. Некий арабский нумеролог сообщает об обычае вырезать числа 220 и 284 на плодах, один из которых влюбленный съедал сам, а другой давал съесть предмету своей страсти, как своего рода математическое средство усиления любовного влечения. Первые теологи отмечали, что в Книге Бытия Иаков отдает в подарок брату своему Исаву 220 животных — «двести коз, двадцать козлов». По мнению теологов, число животных, равное одному из чисел, образующих дружественную пару, свидетельствует о любви Иакова к Исаву.
Вопросы, нерешённые до сих пор
3. Существует ли общая формула, позволяющая описать все пары дружественных чисел?
2. Бесконечно ли количество дружественных чисел?
1. Конечно ли множество пар дружественных чисел?
6. Верна ли гипотеза Брэтли и Мак-Кэй, что все нечетные дружественные числа кратны 3, а сумма чисел, образующую дружественную пару, кратна 9.
Гипотеза Бретли и Мак-Кей
Брэтли и Мак-Кэй выдвинули гипотезу, что все нечетные дружественные числа кратны 3, а сумма чисел, образующих дружественную пару, кратна 9. Никто еще не предложил общей формулы для всех дружественных пар, и неизвестно, конечно или бесконечно число таких пар. В настоящее время известны только две цепочки чисел, которые приводят к исходному числу и имеют 74 1 2 3 4 б 6 7 В 9 10 11 12 13 220 1 184 2 620 Б 020 6 232 10 744 12 285 17 296 63 020 66 928 67 095 69 615 79 750 Таблица 2 284 1 210 2 924 5 564. 6 368 10 856 14 695 18 416 76 084 66 992 71 14Б 87 633 88 730 больше чем два звена.
5. Существуют ли взаимно простые дружественные числа?
4. Существует ли чётно-нечётная пара дружественных чисел?
Дружественные числа
Гипотезы дружественных чисел
4 Гипотеза
Гипотеза 4. Сумма делителей любого числа близка к самому числу.
3 Гипотеза
Гипотеза 3. Сумма делителей нечётного числа обычно меньше самого числа. Вероятность этого для первых 10000 чисел равна 0,24%, для первых 100000 чисел 0,212%, для вторых 100000 – 0,182%, т. е. убывает.
2.Гипотеза
Гипотеза 2. Вероятность того, что сумма делителей чётного числа будет чётной и сумма делителей нечётного числа будет нечётной очень большая, а именно около 95% для четных и 98% для нечётных чисел (для чисел в интервале от 2 до 500). Эта вероятность увеличивается при увеличении числа. Для чисел в интервале от 2 до 100000 эта вероятность для чётных и нечётных чисел соответственно равна 99,24% и 99,69%.
Следствия из гипотез
Следствия из гипотез:
- Ряд долго сохраняет свою чётность (чётность своего первого члена).
- Нечётный ряд быстро распадается (т. е. сходится к 1).
- Чётный ряд распадается медленно.
1.Гипотеза
Гипотеза 1. Дружественный ряд независимо от его первого члена сходится к единице. Проверено для первых 1000 чисел, исключая 30, которые являются членами рядов, начинающихся с чисел 138, 276, 552, 564, 570, 660, 702, 828, 840, 858, 936, 966, 996 (члены этих рядов возрастают до -1 млрд). Среди этой тысячи 3 ряда являются периодическими, которые переходят к совершенным числам (220, 284 и 562).
Используемые интернет ресурсы
- Видео. https://www.youtube.com/watch?v=H_qKmX3JCAQ
- Охота на дружественные числа. http://math4school.ru/ohota_na_druzhestvennie_chisla.html
- Леонард Эйлер. https://interesnyefakty.org/leonard-ejler/
- Леонард Эйлер и Петербургская астрономическая и астрофизическая школа 18 века. http://www.sai.msu.ru/history/euler.html
- Видео о дружественных числах. https://www.youtube.com/watch?v=H_qKmX3JCAQ
- Дружественные числа. https://school-science.ru/5/7/34979
- Дружественные числа. https://yandex.ru/turbo?text=https%3A%2F%2Fsitekid.ru%2Fmatematika%2Fdruzhestvennie_chisla.html
- Пафнутий Львович Чебышёв. http://math4school.ru/chebyshev.html
- П. Л. Чебышёв - гениальный русский математик. https://myfri.org/2019/12/17/pafnutiy-lvovich-chebyishev-genialnyiy-russkiy-matematik/
- Иван Матвеевич Виноградов. http://math4school.ru/vinogradov.html
- Гипотезы дружественных чисел. http://www.hintfox.com/article/gipotezi-dryzhestvennih-chisel.html
Охота на дружественные числа
Вклад русских учёных в изучение дружественных чисел
Пафнутий Львович Чебышев
Следующим математиком после Эйлера, кто пополнил коллекцию дружественных чисел, но только одной парой, был наш выдающийся соотечественник Пафнутий Львович Чебышёв, в 1851 году.
Иван Матвеевич Виноградов
Иван Матвеевич Виноградов – российский и советский математик, директор Математического института им. В.А. Стеклова АН СССР, академик Академии Наук СССР.Родился 2 сентября 1891 года. Виноградов посвятил свою деятельность аналитической теории чисел. Основы этой теории были заложены еще Эйлером, крупные результаты в развитии аналитической теории чисел принадлежат математикам петербургской школы теории чисел, основанной Чебышевым. Виноградову принадлежит решение одной из двух проблем Гольдбаха, которые были поставлены в переписке Гольдбаха с Эйлером в 1742 году. Они формулируются так: каждое четное число, большее или равное 4, является суммой двух простых чисел (бинарная проблема Гольдбаха остается недоказанной до сих пор) и каждое нечетное число большее или равное 7 является суммой трех простых чисел (тернарная проблема Гольдбаха). Эти проблемы не поддавались усилиям крупнейших математиков. И. М. Виноградов решил тернарную проблему Гольдбаха, доказав, что каждое достаточно большое нечетное число представляется суммой трех простых чисел, а также получил формулу, выражающую количество таких представлений. По этой формуле можно узнать, сколькими способами заданное нечетное число может быть разложено на сумму трех простых чисел. При попытке решения проблемы Гольдбаха учёный создал один из самых общих и мощных методов теории чисел – метод тригонометрических сумм.
Ученик Чебышева , занимавшийся теорией чисел
Андрей Андреевич Марков
Андрей Андреевич Марков - русский математик, академик. Внёс большой вклад в математический анализ и теорию чисел. Работы Маркова имеют большое значение. Сюда относится прежде всего магистерская диссертация «О бинарных квадратичных формах положительного определителя» Она примыкала к исследованиям А. Н. Коркина и Е. И. Золотарёв и была высоко оценена П. Л. Чебышёвым. Диссертация посвящена проблеме арифметических минимумов неопределённых бинарных квадратичных форм. В последующих статьях рассматривается проблема арифметических минимумов неопределённых тернарных и кватернарных квадратичных форм. Идеи и результаты А. А. Маркова оказали большое влияние на дальнейшее развитие теории чисел.
Егор Иванович Золотарёв
Егор Иванович Золотарёв - русский математик. Егор Иванович наиболее известен как автор одного из самых простых доказательств закона взаимности, Лемма Золотарёва.
Александр Николаевич Коркин
Александр Николаевич Коркин - русский математик, специалист по дифференциальным уравнениям. Заслуженный профессор Санкт-Петербургского университета. Член Санкт-Петербургского математического общества.
Чебышев об Эйлере
Чебышев писал: "Эйлером было положено начало всех изысканий , составляющих общую теорию чисел".
Леонард Эйлер
Вклад зарубежных учёных в изучение дружественных чисел
Новейшее время
Эльвин Дж. Ли
Следующей рекордной «добычи» достиг американец Элвин Дж. Ли – 300 пар за период с 1968 по 1972 годы. И хотя он оперировал методами Эйлера, в несколько усовершенствованной форме, но при этом пользовался помощью ЭВМ, предшественников современных компьютеров.
Поль Пуле
Первым побил рекорд Эйлера бельгиец Поль Пуле – 62 новые пары к 1948 году.
Новое время
Николо Паганини
В 1866 году, – шестнадцатилетний итальянец Николо Паганини, тезка великого скрипача «изловил» вторую – по величине – пару дружественных чисел: 1 184 и 1 210. Математический мир был потрясён – эту пару, ближайшую к 220 и 284, проглядели все знаменитые математики, изучавшие дружественные числа!
Рене Декарт
Следующую пару дружественных чисел открыл в 1638 году Рене Декарт. В результате вычислений он получил пару чисел: 9 363 584 и 9 437 056.
Пьер Ферма
Независимо от ибн аль-Банна, спустя более чем 300 лет, в 1636 году, эту же пару 17 296 и 18 416 открыл Пьер Ферма. Пьер Ферма - французский математик - самоучка, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. Родился 17 августа 1601 года в городке Бомон-де-Ломань.
Средние века
Ибн аль -Банна
Пару дружественных чисел 17 296 и 18 416 открыл марокканский ученый ибн аль-Банна, около 1300 года. Уже в ХХ веке в одном из трактатов этого арабского ученого были обнаружены следующие строки: "Числа 17 296 и 18 416 являются дружественными; одно из них избыточно, другое недостаточно. Аллах всеведущ".
Абу-Хасан Сабит ибн Курра
Один из способов получения дружественных чисел указал еще в IX веке, примерно в 850 году, арабский математик Абу-Хасан Сабит ибн Курра ибн Марван аль-Харрани. Найденный Сабитом способ получения дружественных чисел звучит так: Если для натурального числа n > 1 все три числа:
p = 3 · 2n – 1 – 1,
q = 3 · 2n – 1,
r = 9 · 22n – 1 – 1,
являются простыми, то числа 2n · pq и 2n · r образуют пару дружественных чисел. Эта формула даёт пары 220 и 284, 17 296 и 18 416, 9 363 584 и 9 437 056 соответственно для n = 2, 4, 7, но больше никаких пар дружественных чисел для n < 20000 не существует. Кроме того, многие дружественные числа, например 6 232 и 6 368, не могут быть получены по этой формуле. Сабит получил лишь уже известную пифагорову пару дружественных чисел. Использовал ли он свою правило для отыскания дружественных чисел при n > 2, неизвестно.
Античный мир
Пифагор
Однажды Пифагор на вопрос, кого следует считать другом, ответил так: «Того, кто является моим вторым я, как числа 220 и 284». Видимо, какое – то необычное свойство сблизило эти числа настолько, что сам Пифагор признал их парой дружественных чисел. Считается, что именно Пифагор и был первооткрывателем этой пары дружественных чисел - первой, наименьшей из возможных и единственно известной на протяжении более чем 15 последующих веков.