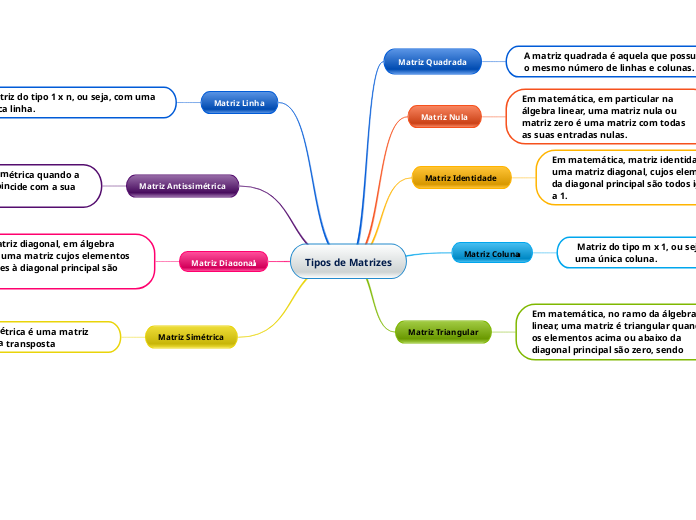
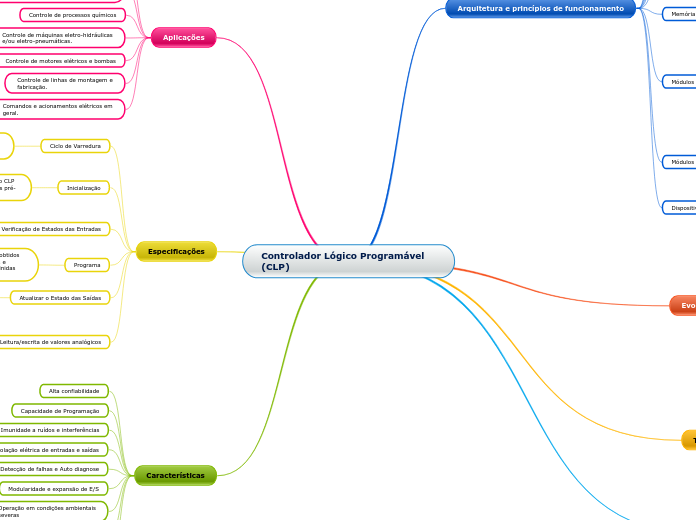
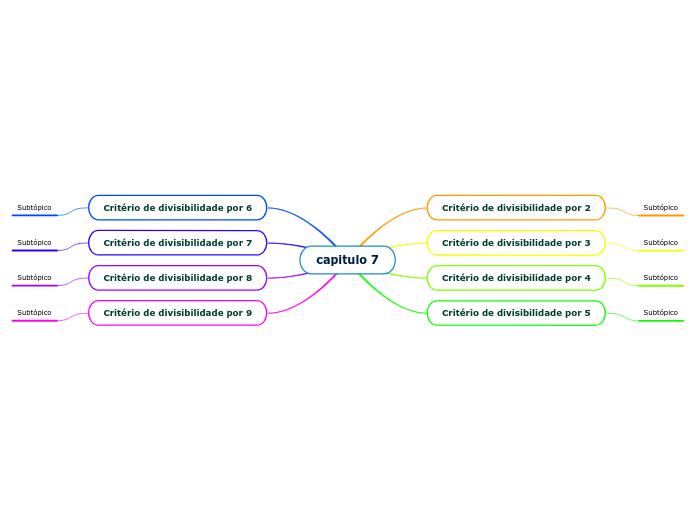
Conjugado de um Número Complexo
Representação Geométrica de um Número Complexo
P= a + bi é representado por P= (a, b)
Divisão
Multiplicação
Dados dois números complexos, z1 e z2, para determinar z3 = z1 . z2 devemos aplicar a propriedade distributiva, lembrando que i2 = -1, e depois reduzir os "termos semelhantes".
Adição e Subtração
Para somar dois números complexos devemos somar separadamente suas partes reais e suas partes imaginárias. A mesma ideia se aplica à subtração.
Operações com Números Complexos
Quando Re(z)=0 e Im(z) diferente de zero, z é um número imaginário puro
Quando Im(z)=0, z é um número real
Forma Algébrica do Número Complexo
Z= a + bi
O número real a é chamado parte real de Z e o número real b é chamado parte imaginária de Z. Indica-se por:
a = Re(z) e b = Im(z)
Dizemos que i é uma raiz quadrada de -1 (unidade imaginária)
Assim:
i2 = -1
A novidade é que "o quadrado de certo elemento é igual a um número negativo"
Cartografia
Aplicações
Astronomia
Análise de corrente elétrica
Teoria da Relatividade de Einstein
Na teoria do buraco negro feita pelo cientista Stephen Hawking
História dos Números Complexos
Números Complexos
Aritmética