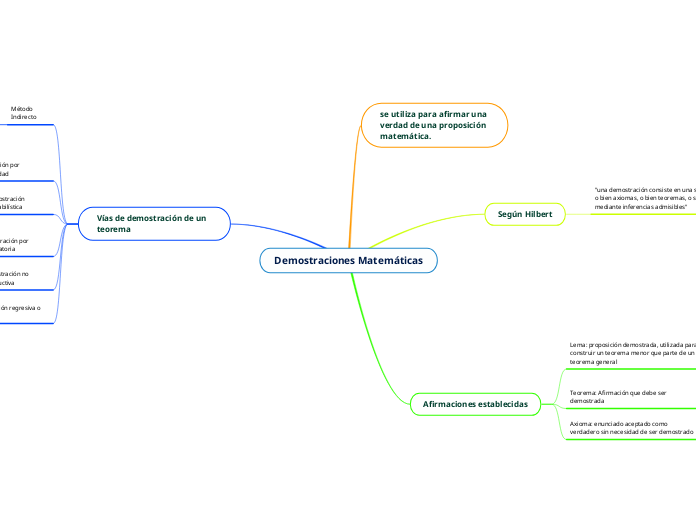
Demostraciones Matemáticas
En el ámbito matemático, una demostración es una secuencia de fórmulas que derivan de axiomas o teoremas mediante inferencias válidas, con el fin de validar una proposición. Existen varias metodologías para demostrar teoremas.
開啟
Demostraciones Matemáticas Vías de demostración de un teorema Demostración regresiva o progresiva se caracteriza por partir de la hipótesis y llegar directamente a la tesis o conclusión Demostración no constructiva un objeto con una propiedad existe sin explicar cómo tal objeto se puede encontrar. Demostración por combinatoria establece igualdad de expresiones desiguales al mostrar que cuentan para el mismo objeto en de formas distintas. Demostración probabilística Se muestra que un ejemplo existe usando métodos probabilísticos. este no conduce a una demostración demostración por exhaustividad se constituye al fraccionar un numero finito de casos y experimentar cada uno por individual Método Indirecto de lo que se concluye la tesis del teorema es verdadero radica en negar tesis del teorema, con esta proposición y las reglas de la lógica y en la teoría se tiene que hallar una contradicción. Afirmaciones establecidas Axioma: enunciado aceptado como verdadero sin necesidad de ser demostrado Teorema: Afirmación que debe ser demostrada Corolario: conclusión de un teorema ya demostrado Lema: proposición demostrada, utilizada para construir un teorema menor que parte de un teorema general Según Hilbert "una demostración consiste en una sucesión de formulas que, o bien axiomas, o bien teoremas, o se han obtenidos estas mediante inferencias admisibles" se utiliza para afirmar una verdad de una proposición matemática.
