ECUACIÓN CUADRÁTICA

更多类似内容

PROPIEDADES QUÍMICAS Y FÍSICAS DE LAS SOLUCIONES.

由NICOLE NALLIBE ZAMBRANO LOPEZ

FUNCIONES REALES DE VARIABLE REAL

由Betuel Castillo

PENSAMIENTO COMPUTACIONAL EN INFANTIL

由MARIA LUISA SERRANO MARTINEZ

PROACTIVIDAD

由Caterin Fonseca

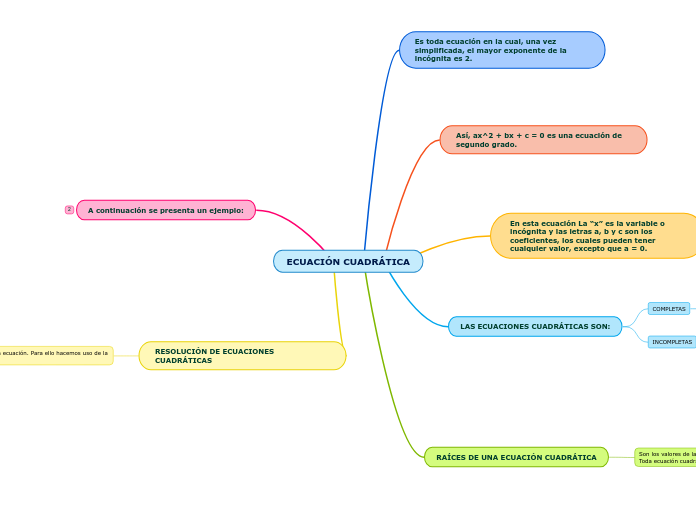
ECUACIÓN CUADRÁTICA

RESOLUCIÓN DE ECUACIONES CUADRÁTICAS

Es hallar las raíces de la ecuación. Para ello hacemos uso de la fórmula:

El “±” expresa que la ecuación tiene ¡DOS SOLUCIONES! La parte “b2 – 4ac” se le denomina discriminante:

* Si es positivo, hay DOS soluciones * Si es cero sólo hay UNA solución, * y si es negativo hay dos soluciones que incluyen números imaginarios.

x = [ – b ± √(b^2 – 4ac) ] / 2a

A continuación se presenta un ejemplo:

Los coeficientes son: a = 1; b = – 12 y c = 36. Los sustituimos en la fórmula: x = [ – b ± √(b^2 – 4ac) ] / 2a → x = {- (-12) ± √[(-12)2 – 4(1)(36)] } / [2(1)] Resolvemos x = {12 ± √ [144 – 144] } / 2 = 12 / 2 = 6 x1 = x2 = 6

Resolver la ecuación cuadrática x2 – 12x + 36 = 0.

RAÍCES DE UNA ECUACIÓN CUADRÁTICA

Son los valores de la incógnita que satisfacen la ecuación. Toda ecuación cuadrática tiene dos raíces.

LAS ECUACIONES CUADRÁTICAS SON:

INCOMPLETAS

Son ecuaciones de la forma ax^2 + c = 0 que carecen del término x o de la forma ax^2 + bx = 0 que carecen del término independiente. Así, 2x2 + 3 = 0 y 2x2 + 5x son ecuaciones cuadráticas incompletas.

COMPLETAS

Son ecuaciones de la forma ax^2 + bx + c = 0 que tienen un término x2, un término x y un término independiente de x. Así, 2x2 + 5x + 3 = 0 es una ecuación cuadrática completa.

En esta ecuación La “x” es la variable o incógnita y las letras a, b y c son los coeficientes, los cuales pueden tener cualquier valor, excepto que a = 0.

Así, ax^2 + bx + c = 0 es una ecuación de segundo grado.

Es toda ecuación en la cual, una vez simplificada, el mayor exponente de la incógnita es 2.