作者:Cristian Robayo Alfonso 4 年以前
263
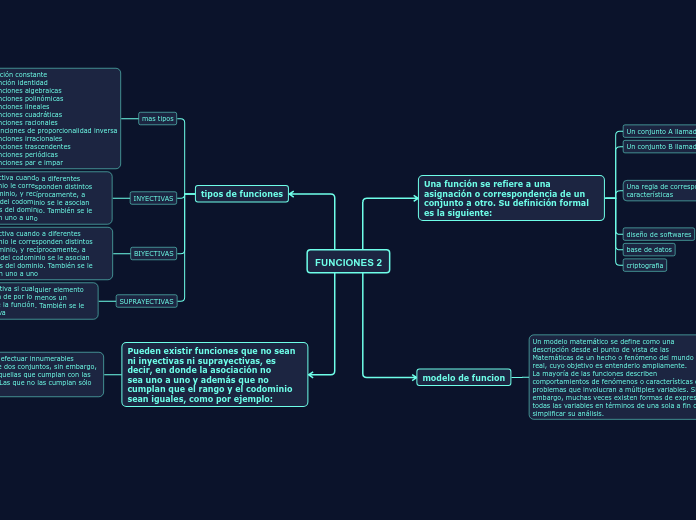
FUNCIONES 2
En el campo de las matemáticas, una función es una regla que asigna elementos de un conjunto a elementos de otro conjunto, siguiendo ciertas características precisas. No todas las correspondencias entre conjuntos son funciones; solo lo son aquellas que cumplen con las condiciones especificadas.