Notas de clase sobre series de potencias
Notas:
https://www.canva.com/design/DAEtSKgbzNM/5ffntZr2PeURx9y0cdvLjQ/view?utm_content=DAEtSKgbzNM&utm_campaign=designshare&utm_medium=link&utm_source=sharebutton
Referencias:
https://www.giematic.unican.es/index.php/series/seriespot/seriespot-defbas
https://www.etsist.upm.es/uploaded/docs_personales/hernandez_heredero_rafael_jose/old/CalI/CIT5.pdf
Convergencia
La convergencia de una serie de potencias es uniforme en el interior de su intervalo de convergencia. Esto implica que cualquier función f (x) definida por una serie de potencias tiene que tener una gran regularidad, al ser los términos anx
n funciones muy regulares.
El primer paso en el estudio de series de potencias es determinar su región
de convergencia. Usando el criterio de comparación con una serie geométrica,
podemos demostrar el siguiente resultado.
Teorema de Abel
Se considera la serie ∑∞n=0an(x−a)n.
Entonces se cumple una y sólo una de las afirmaciones siguientes:
a) La serie converge sólo en el punto a.
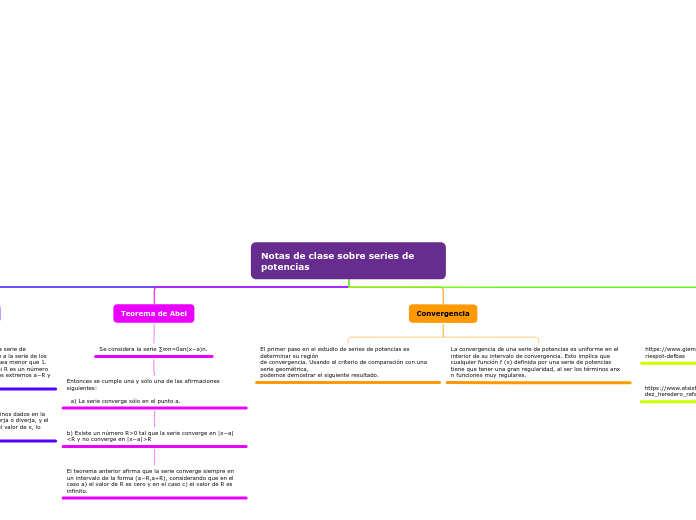
b) Existe un número R>0 tal que la serie converge en |x−a|R
El teorema anterior afirma que la serie converge siempre en un intervalo de la forma (a−R,a+R), considerando que en el caso a) el valor de R es cero y en el caso c) el valor de R es infinito.
Características
Para obtener el radio de convergencia de una serie de potencias, R, se aplica el criterio del cociente a la serie de los valores absolutos y se impone que el límite sea menor que 1. Una vez obtenido el radio de convergencia, si R es un número real no nulo, se analiza la convergencia en los extremos a−R y a+R.
Una serie de potencias es una suma de términos dados en la forma general aₙ(x-a)ⁿ. Que esta serie converja o diverja, y el valor al cual converge o diverge, depende del valor de x, lo cual hace a la serie una función.
¿ Qué son ?
Definición(Serie de potencias).- Una expresión de la forma:
∑n=0∞an(x−a)n
recibe el nombre de serie de potencias centrada en el punto a.
