作者:brayan farfan 3 年以前
249
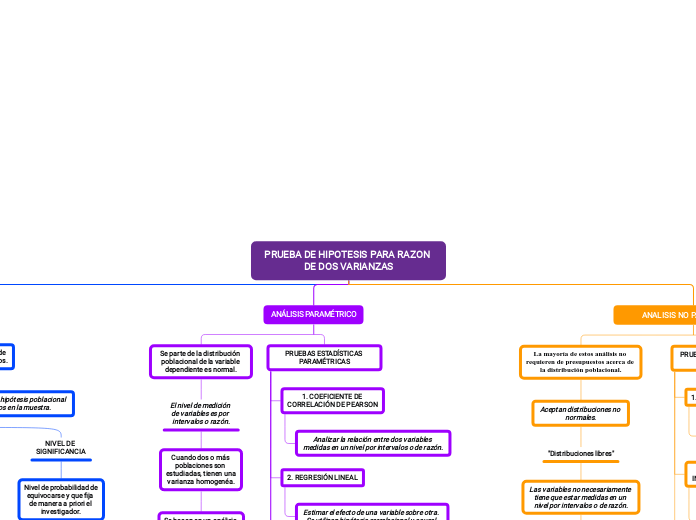
PRUEBA DE HIPOTESIS PARA RAZON DE DOS VARIANZAS
作者:brayan farfan 3 年以前
249

更多类似内容
Los individuos, casos o unidades de análisis de la muestra pueden ordenarse por rangos, se utilizan para relacionar escalas tipo Likert.
Son medidas de correlación para variables en un nivel de medición ordinal.
Evaluar si las variables incluidas en la tabla de contingencia o tabulación cruzada están correlacionadas
Evaluar la hipótesis acerca de la relación entre dos variables categóricas.
"Distribuciones libres"
Las variables no necesariamente tiene que estar medidas en un nivel por intervalos o de razón.
Se aplican en variables categóricas.
Se utilizan para muestras pequeñas.
Las hipótesis se basan en rangos, mediana y frecuencia de datos.
Analiza si más de dos grupos difieren significativamente entre sí en cuanto a sus medias y varianzas.
Analizar si dos proporciones o porcentajes difieren significativamente entre sí.
Evalúa si dos grupos difieren entre sí de manera significativa respecto a sus medias en una variable.
Estimar el efecto de una variable sobre otra. Se utilizan hipótesis correlacional y causal.
Analizar la relación entre dos variables medidas en un nivel por intervalos o de razón.
Cuando dos o más poblaciones son estudiadas, tienen una varianza homogenéa.
Se basan en un análisis en el tipo de hipótesis y los niveles de medición de las variables.
Se utilizan para muestras grandes.
NIVEL DE SIGNIFICANCIA
Nivel de probabilidad de equivocarse y que fija de manera a priori el investigador.
1. Nivel de significancia de 0.05. 95% de seguridad para generalizar sin equivocarse y 5% en contra.
2. Nivel de significancia de 0.01. 99% en su favor y 1% en contra. (0.99 y 0.01=100)
DISTRIBUCIÓN MUESTRAL
Conjunto de valores sobre una estadística calculada de todas las muestras posibles de una población.
DISTRIBUCIÓN NORMAL
Es unimodal, asimetría a cero y mesocúrtica.
Es la distribución en forma de campana que se logra con muestras de 100 o más unidades.