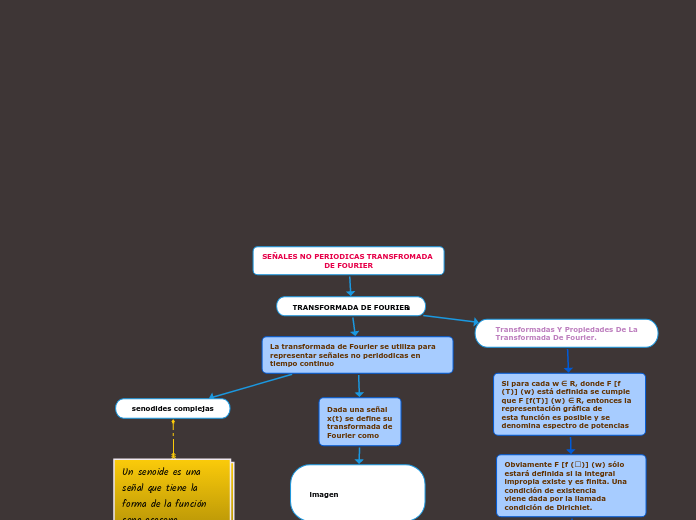
SEÑALES NO PERIODICAS TRANSFROMADA DE FOURIER

更多类似内容

El problema de Dios

由Mathew Clavijo

división de la filosofía

由Ana victoria Mercado alfaro

Los fundamentos de la dignidad de la persona humana / ¿QUIÉN SOY YO?

由Belen Martinez

GNU.LINUX

由WILSON NOREÑA

imagen

Donde K(T,t) recibe el nombre de kernel de la transformación, y los límites a y b están dados por la transformada correspondiente.

Para que exista, s=jω tiene que estar dentro de la ROCx

La CTFT de la señal x(t) existirá siempre que se cumplan unascondiciones similares a las de existencia de la CTFS:

x(t) debe ser absolutamente integrable

x(t) debe tener un nº finito de discontinuidades en cualquier intervalo finito

x(t) debe tener un nº finito de oscilaciones en cualquier intervalo finito

Dada una señal x(t) se define su transformada de Fourier como

senodides complejas

Un senoide es una señal que tiene la forma de la función seno ocoseno.

La transformada de Fourier se utiliza para representar señales no peridodicas en tiempo continuo

TRANSFORMADA DE FOURIER

Transformadas Y Propiedades De La Transformada De Fourier.

Si para cada w ∈ R, donde F [f (T)] (w) está definida se cumple que F [f(T)] (w) ∈ R, entonces la representación gráfica de esta función es posible y se denomina espectro de potencias

Obviamente F [f ()] (w) sólo estará definida si la integral impropia existe y es finita. Una condición de existencia viene dada por la llamada condición de Dirichlet.

IMAGEN

SEÑALES NO PERIODICAS TRANSFROMADA DE FOURIER