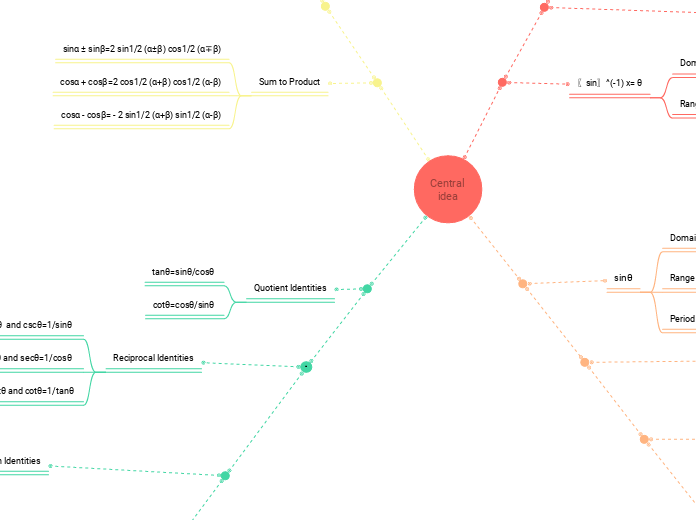
Spider Diagram

更多类似内容

JavaScript

由Brenda De la Cruz

typo3_doc_tsref

由David Lanier

The 6 trigonometric Functions

由Thang-Dung Martin

ANTIBODY AND ANTIGEN

由Yolanda Soto

SOH - CAH - TOA

a function f is even if f(-x) = f(x) and odd if f(-x) = -f(x)

Central idea

Quotient Identities

cot⁡θ=cos⁡θ/sin⁡θ

tan⁡θ=sin⁡θ/cos⁡θ

Reciprocal Identities

tan⁡θ=1/cot⁡θ and cot⁡θ=1/tan⁡θ

cos⁡θ=1/sec⁡θ and sec⁡θ=1/cos⁡θ

sin⁡θ=1/csc⁡θ and csc⁡θ=1/sin⁡θ

Pythagorean Identities

〖csc〗^2 θ-〖cot〗^2 θ=1^

〖sec〗^2 θ-〖tan〗^2 θ=1^

〖sin〗^2 θ+〖cos〗^2 θ=1^

Half Angle Identities

tan^2(⁡θ) = (1 - cos2⁡θ) / (1 + cos2θ)

cos^2(θ) = (1 + cos2θ)/2

sin^2(θ) = (1 - cos2⁡θ)/2

Double Angle Identities

tan2⁡θ = 2tan⁡θ / 1 - tan^2(⁡θ)

cos(2⁡θ) = 1 - 2sin^2(⁡θ)

cos(2⁡θ) = 2 cos^2 (⁡θ) - 1

cos(2⁡θ) = cos⁡^2⁡(θ) - sin^2(⁡θ)

sin(2θ) = 2sin⁡θ cos⁡θ

Sum/Difference Identities

tan⁡(α±β) = (tanα ± tanβ)/(1 ∓ tanαtanβ)

cos(α±β) = cosα cos⁡β ∓ sinα sinβ

sin⁡(α±β) = sin⁡α cos⁡β ± cosα sinβ

Cofunction Identities

csc(π/2-θ)=secθ and sec(π/2-θ)=cscθ

tan(π/2-θ)=cotθ and cot(π/2-θ)=tanθ

sin(π/2-θ)=cosθ and cos(π/2-θ)=sinθ

Even/Odd Identities

sec(-θ)=secθ

csc(-θ)=-cscθ

cot(-θ)=-cotθ

tan(-θ)=-tanθ

sin(-θ)=-sinθ

cos(-θ)=cosθ

Sum to Product

cosα - cos⁡β= - 2 sin⁡1/2 (α+β) sin⁡1/2 (α-β)

cosα + cos⁡β=2 cos⁡1/2 (α+β) cos⁡1/2 (α-β)

sin⁡α ± sin⁡β=2 sin⁡1/2 (α±β) cos⁡1/2 (α∓β)

Product to Sum

cos⁡α sin⁡β=1/2 [ sin⁡(α+β) - sin⁡(α-β) ]

sin⁡α cos⁡β=1/2 [ sin⁡(α+β) + sin⁡(α-β) ]

cos⁡α cos⁡β=1/2 [ cos⁡(α-β) + cos⁡(α+β) ]

sin⁡α sin⁡β=1/2 [ cos⁡(α-β) - cos⁡(α+β) ]

sinθ

cosθ

[-1,+1]

tanθ

(-∞,+∞)

secθ

R-(2n+1)π/2

cscθ

2π

(-∞,-1]∪[+1,+∞)

cotθ

Period

π

R-nπ

[-π/2, π/2]

〖cos〗^(-1) x= θ

[0, π]

[-1,1]

〖tan〗^(-1) x= θ

(-π/2, π/2)

〖sin〗^(-1) x= θ

[0, π], θ≠π/2

〖csc〗^(-1) x= θ

[-π/2, π/2], θ≠0

(-∞,-1]∪[1,+∞)

〖cot〗^(-1) x= θ

Range

(0, π)

Domain

(-∞,+∞)