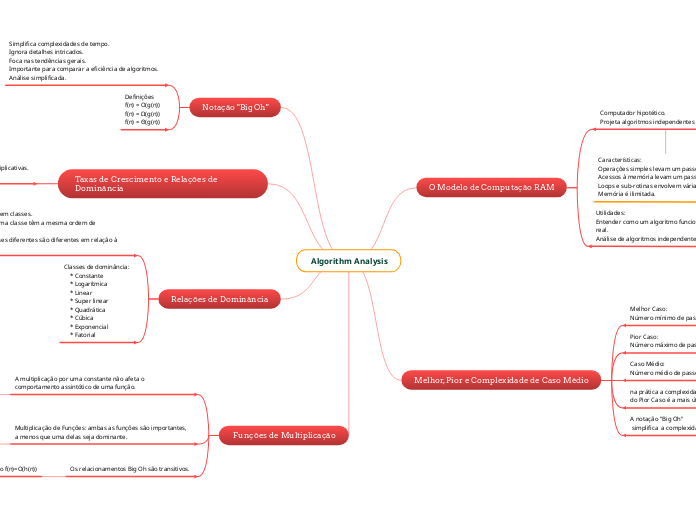
Algorithm Analysis

Computador hipotético.
Projeta algoritmos independentes de máquina.

Características:
Operações simples levam um passo de tempo.
Acessos à memória levam um passo de tempo.
Loops e sub-rotinas envolvem várias operações.
Memória é ilimitada.

Utilidades:
Entender como um algoritmo funcionará em um computador real.
Análise de algoritmos independente da máquina.

Melhor Caso:
Número mínimo de passos.

Pior Caso:
Número máximo de passos.

Caso Médio:
Número médio de passos.

na prática a complexidade
do Pior Caso é a mais útil.

A notação "Big Oh"
simplifica a complexidades de tempo.

Simplifica complexidades de tempo.
Ignora detalhes intricados.
Foca nas tendências gerais.
Importante para comparar a eficiência de algoritmos.
Análise simplificada.

Definições
f(n) = O(g(n))
f(n) = Ω(g(n))
f(n) = Θ(g(n))

Ignora as diferenças entre constantes multiplicativas.
As diferenças não afetam o crescimento.

Agrupa funções em classes.
Funções da mesma classe têm a mesma ordem de crescimento.
Funções de classes diferentes são diferentes em relação à notação.

Classes de dominância:
* Constante
* Logarítmica
* Linear
* Super linear
* Quadrática
* Cúbica
* Exponencial
* Fatorial

A multiplicação por uma constante não afeta o comportamento assintótico de uma função.

Multiplicação por constante
* O(c · f(n)) → O(f(n))
* Ω(c · f(n)) → Ω(f(n))
* Θ(c · f(n)) → Θ(f(n))

Multiplicação de Funções: ambas as funções são importantes, a menos que uma delas seja dominante.

Multiplicação por funções
* O(f(n))*O(g(n)) → O(f(n)*g(n))
* Ω(f(n))*Ω(g(n)) → Ω(f(n)*g(n))
* Θ(f(n))* Θ(g(n)) → Θ(f(n)*g(n))

Os relacionamentos Big Oh são transitivos.

Transitividade
* Se f(n)=O(g(n)) e g(n)=O(h(n)), então f(n)=O(h(n))