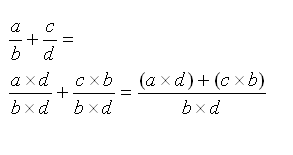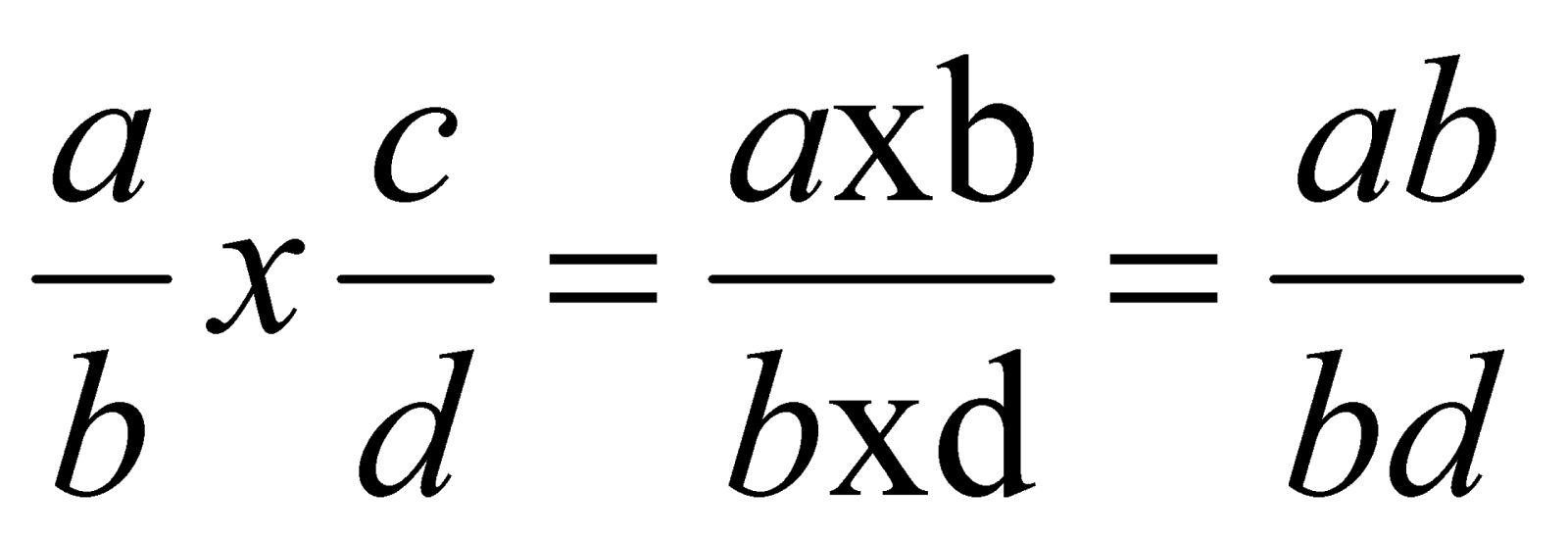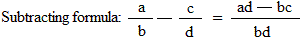Fractions

Adding fractions requires that the denominator in all of the fractions that are being added together are the same. If the demoninators are not the same, the LCM (least common multiple) of the denominators need to be found. Watever factor the denominator needs to be multiplied by, the numerator needs to be multiplied by that factor as well. Once the denominators are the same, the numerators can be added together. (We will take a look at an example of this in the example branch)

The formula for adding fractions.

Practice problem for solving an addition problem with fractions. This example shows how a common denominator is needed in order to add the fractions.

This is a video on adding fractions. The video works step by step so that a student should be able to follow along.

This is a fruit popping game that students need to get fraction addition problems right in order to pop the fruit with the right answer. The game has many different levels and settings depending on how advanced a person wants it.

This soccer fraction addition game allows players to pracitce problems according to the difficultly level selected. When a problem is answered incorrectly, a guided solution follows.

Unlike adding and subtracting fractions, we do not need to find a common denominator when multiplying fractions. The numerators of all of the fractions that are being multiplied together are mutiplied to give a final product in the numerator position. The denominators of all of the fractions that are being multiplied together are multiplied to give a final product in the numerator postition. (We will take a look at an example of this in the example branch)

The formula for multiplying fractions.

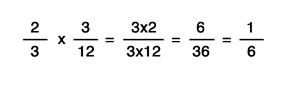
Practice problem for solving a multiplication problem with fractions. This example shows how the numerators and denominators are multiplied together.

This is a video on multiplying fractions. The video works step by step so that a student should be able to follow along.

Multiplication game where you race amongst other sleds to try to be the first to the finish line by getting multiplication problems correct.

Subtracting fractions requires that the denominator in all of the fractions that are being added together are the same. If the demoninators are not the same, the LCM (least common multiple) of the denominators need to be found. Watever factor the denominator needs to be multiplied by, the numerator needs to be multiplied by that factor as well. Once the denominators are the same, the numerators can be subtracted from each other. (We will take a look at an example of this in the example branch)

The formula for subtracting fractions.

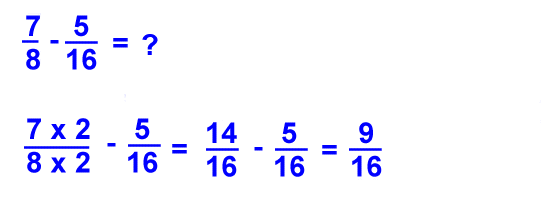
Practice problem for solving a subtraction problem with fractions. This example shows how a common denominator is needed in order to subtract the fractions.

This is a video on subtracting fractions. The video works step by step so that a student should be able to follow along.

This is a practice activity where students are able to try out a ton of fraction subtraction problems on their own.

A winter fraction subtraction game where the goal is to try and see how many problems can be answered right in the time allowed.

When dividing fractions, there are three different situations that need to be considered. The common-numerator rule states that a/b / a/c = c/b. This is the case becuause when a/b is multiplied by the reciprocal of a/c, which is c/a, the a's cancel out. The common denominator rule a/b / c/b = a/c. This is the case because when a/b is multiplied by the reciprocal of c/b, which is b/c, the b's cancel out. The invert-and-multiply rules states that a/b / c/d = a/b x d/c.

The formula for dividing fractions.

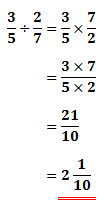
Practice problem for solving an division problem with fractions. This example shows how a reciprocal is used in order to turn the problem into a multiplication problem.

This is a video on dividing fractions. The video works step by step so that a student should be able to follow along.

This is a fraction division game that is centered around the game of basketball. You get to try to make the basketball in the basket and then in order for the point to count, a fraction problem needs to be answered correctly.

This site allows you to practice fraction division problems on your own. There is a guided solution provided to assist in solving the problems.