AlfabetosAlfabetos, Cadenas y Lenguajes
Alfabeto
Un alfabeto es un conjunto finito no vacío de símbolos y se denota como Sigma.
Lenguaje
Un lenguaje L es un conjunto de cadenas sobre un alfabeto Sigma definido, éstas pueden ser cualquier cadena w.
Operaciones con lenguajes
Concatenación
El concepto de concatenación se puede extender a los lenguajes. Se define la concatenación de lenguajes como sigue
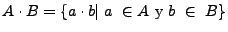
El lenguaje que resulta de la concatenación de A y B esta formado por la concatenación de todas la cadenas de A con todas la cadenas de B.
Ejemplo: Si A={hola, adios} y B={casa}, entonces, A.B={holacasa, adioscasa}.
Potencia
La definición de potencia, también puede extenderse a los lenguajes de la misma manera
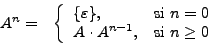
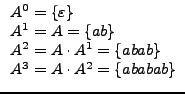
Por lo tanto, si A={ab} sobre un algún alfabeto, se tiene que:
Dado que los lenguajes son conjuntos de cadenas, las operaciones, intersección, unión y sublenguaje se difinen como sigue:
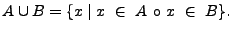
Unión
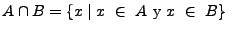
Intersección
Inverso
El inverso de un lenguaje se denota como A^I y su efecto sobre el lenguaje es que todas las cadenas del lenguaje se invierten, esto es, si A es un lenguaje, su inverso es:
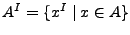
Ejemplo: Si A={hola,raro}, entonces A^I={aloh,orar}
Cadena
Una cadena o palabra es una secuencia finita de símbolos que pertenecen a un alfabeto y comunmente se denota con la letra w. La cadena vacía se denota como epsilon y es una secuencia vacía de símbolos tomados de cualquier alfabeto Sigma
Operaciones con Cadenas
Concatenación
Si w1 y w2 son cadenas, la concatenación de éstas dos cadenas resulta en la cadena que se obtiene al agregar la segunda al final de la primera, es decir, si tenemos w1=mesa y w_2=banco, la concatenación de estas dos cadenas es mesabanco y se denota w1.w2 o w1w2, por lo que podemos observar que |w1+w2|=|w1|+|w2|.
La concatenación de cualquier cadena w1 con la cadena vacía epsilon deja intacta a la cadena w1.
La igualdad entre cadenas se denota con el signo '=' y se dá cuando dos o más cadenas tienen exactamente los mismos símbolos en la misma posición y tienen la misma longitud.
Potencia
La potencia de una cadena sobre un alfabeto quiere decir que tomamos toda la cadena como una unidad atómica, es decir, si w=abc, entonces w^2=ww, w^3=www y así sucesivamente
Por lo tanto si w=ab sobre el alfabeto Sigma={a,b}, tenemos que:
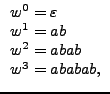
Inversa
La inversa o transpuesta de una cadena w se denota como w^I y quiere decir que, si se tiene w=taza, entonces w^I=azat
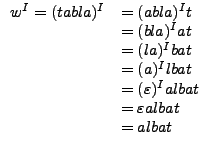
Lenguaje Universal
Un lenguaje universal sobre algún alfabeto Sigma, o cerradura de Sigma, es el lenguaje que contiene todas las cadenas que es posible formar con los símbolos de Sigma y se denota como Sigma^*