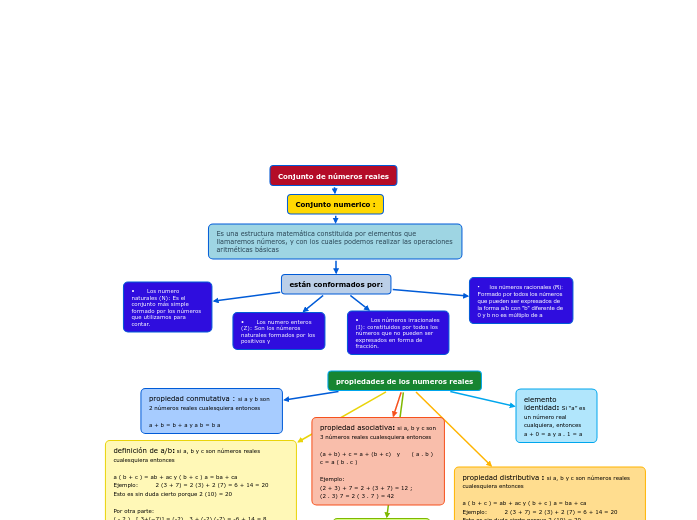
Conjunto de números reales
Es una estructura matemática constituida por elementos que llamaremos números, y con los cuales podemos realizar las operaciones aritméticas básicas
• Los números irracionales (I): constituidos por todos los números que no pueden ser expresados en forma de fracción.
• Los numero naturales (N): Es el conjunto más simple formado por los números que utilizamos para contar.
• Los numero enteros (Z): Son los números naturales formados por los positivos y
• los números racionales (R): Formado por todos los números que pueden ser expresados de la forma a/b con "b" diferente de 0 y b no es múltiplo de a
propiedades de los numeros reales
propiedad conmutativa : si a y b son 2 números reales cualesquiera entonces
a + b = b + a y a b = b a
propiedad asociativa: si a, b y c son 3 números reales cualesquiera entonces
(a + b) + c = a + (b + c) y ( a . b ) c = a ( b . c )
Ejemplo:
(2 + 3) + 7 = 2 + (3 + 7) = 12 ; (2 . 3) 7 = 2 ( 3 . 7 ) = 42
propiedad distributiva : si a, b y c son números reales cualesquiera entonces
a ( b + c ) = ab + ac y ( b + c ) a = ba + ca
Ejemplo: 2 (3 + 7) = 2 (3) + 2 (7) = 6 + 14 = 20
Esto es sin duda cierto porque 2 (10) = 20
Por otra parte:
( - 2 ) . [ 3+(−7)] = (-2) . 3 + (-2) (-7) = -6 + 14 = 8
Ó
( - 2 ) . [ 3+(−7)] = (-2) . 10 = -2 + 10 = 8
elemento identidad: Si “a” es un número real cualquiera, entonces
a + 0 = a y a . 1 = a
inverso: Si “a” es un número real arbitrario, entonces existe un único número denominado el negativo de “a”
a + ( - a ) = 0 𝑎 .𝑎−1
definición de a/b: si a, b y c son números reales cualesquiera entonces
a ( b + c ) = ab + ac y ( b + c ) a = ba + ca
Ejemplo: 2 (3 + 7) = 2 (3) + 2 (7) = 6 + 14 = 20
Esto es sin duda cierto porque 2 (10) = 20
Por otra parte:
( - 2 ) . [ 3+(−7)] = (-2) . 3 + (-2) (-7) = -6 + 14 = 8
Ó
( - 2 ) . [ 3+(−7)] = (-2) . 10 = -2 + 10 = 8