Мера множеств
Виды мер множеств
Мера Лебега

Вероятность

Мера Жордана
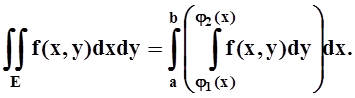
Мера Хаусдорфа
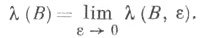
Мера Стилтьеса

Мера Бореля

Мера Хаара

Мера
Определение
Общее название различных типов обобщений понятий Евклидовой длины, площади и n-мерного объёма для более общих пространств.
Мерой называется функция множества μ(A), заданная на полукольце множеств, принимающая неотрицательные вещественные значения и обладающая свойством аддитивности: для любого конечного разложения множества на объединение попарно непересекающихся множеств
A = A1 ∪ A2 ∪ . . . ∪ An
имеет место равенство
μ(A) = ∑μ(Ak).
Продолжение меры с полукольца на кольцо

Счётная аддитивность

Лебегово продолжение меры
Случай полукольца с единицей

Случай полукольца без единицы
Расширение понятия измеримости в случае σ-конечной меры
Измеримые функции
Определения и основные свойства
Арифметические операции над измеримыми функциями
Эквивалентные функции, сходимость почти всюду
Теорема Егорова
Сходимость по мере
Теорема Лузина