Desarrollos alternativos en
Raíces de Ecuaciones.
PROPORCION AUREA
logra exactitudes muy por debajo de
la lograda con el Método de Regla
Falsa, siendo éste lógicamente, más acelerado.
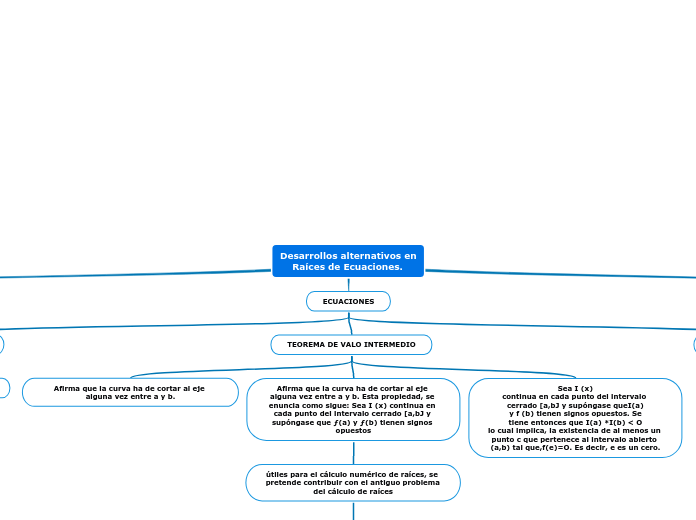
ECUACIONES
METODO REGLA FALSA
C=aƒ(b)-bƒ(a)/ƒ(b)-ƒ(a)
TEOREMA DE VALO INTERMEDIO
Afirma que la curva ha de cortar al eje alguna vez entre a y b.
Afirma que la curva ha de cortar al eje alguna vez entre a y b. Esta propiedad, se enuncia como sigue: Sea I (x) continua en cada punto del intervalo cerrado [a,bJ y supóngase que ƒ(a) y ƒ(b) tienen signos opuestos
útiles para el cálculo numérico de raíces, se pretende contribuir con el antiguo problema del cálculo de raíces
CLASIFICACIÓN DE LOS METODOS
Los procedimientos numéricos
iterativos, utilizados para el cálculo
numérico de raíces de ecuaciones
Sea I (x)
continua en cada punto del intervalo cerrado [a,bJ y supóngase queI(a)
y f (b) tienen signos opuestos. Se
tiene entonces que I(a) *I(b) < O
lo cual implica, la existencia de al menos un punto c que pertenece al intervalo abierto (a,b) tal que,f(e)=O. Es decir, e es un cero.
ITERACIÓN PUNTO FIJO
Xi+l = g(Xi)
ALTERNATIVOS
POSICION ALEATORIA
obtendrán resultados distintos del
valor de la raíz. Recuérdese también, que él realiza la búsqueda de
manera aleatoria dentro del intervalo