Стереометрія
Стереометрія — це розділ геометрії, у якому вивчаються фігури у просторі.Основними фігурами у просторі є точка, пряма і площина.Аксіоми стереометрії – це основні властивості основних фігур стереометрії. Є три основних аксіоми:А1. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй.А2. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій яка проходить через цю точку.А3. Якщо дві різні прямі перетинаються, то через них можна провести площину, і до того ж тільки одну.
Площа
Площа геометричної фігури -числова характеристика геометричної фігури, яка показує розміри цієї фігури (частини поверхні, обмеженої замкнутим контуром даної фігури).Площа поверхні куба дорівнює квадрату довжини його грані помноженому на шість.Формула площі куба:S = 6 a2де S - площа куба,a - довжина грані куба.Площа прямокутного паралелепіпедаS = 2(a · b + a · h + b · h)де S - площа прямокутного паралелепіпеда,a - довжина,b - ширина,h - висота.
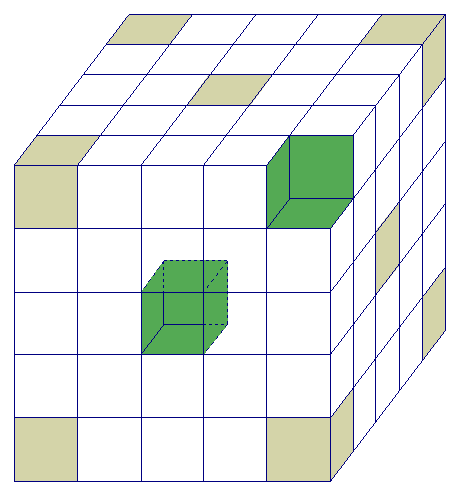
Об'єм
Об'єм геометричної фігури - кількісна характеристика простору, яке займає тіло або речовина. Об'єм тіла або його місткість визначається формою та лінійними розмірами цього тіла.Властивості (аксіоми) об’єму многогранників:рівні многогранники мають рівні об’єми;якщо многогранник складений із кількох многогранників, то його об’єм дорівнює сумі об’ємів цих многогранників;об’єм куба з ребром, що дорівнює одиниці довжини, дорівнює одиниці об’єму.Рівновеликими називають тіла з однаковими об’ємами.Рівноскладеними називають тіла, які складені з одних і тих самих многогранників.Будь-які рівноскладені тіла мають рівні об’єми (за другою властивістю). Обернене твердження не є правильним (на відміну від аналогічної теореми для площ).
a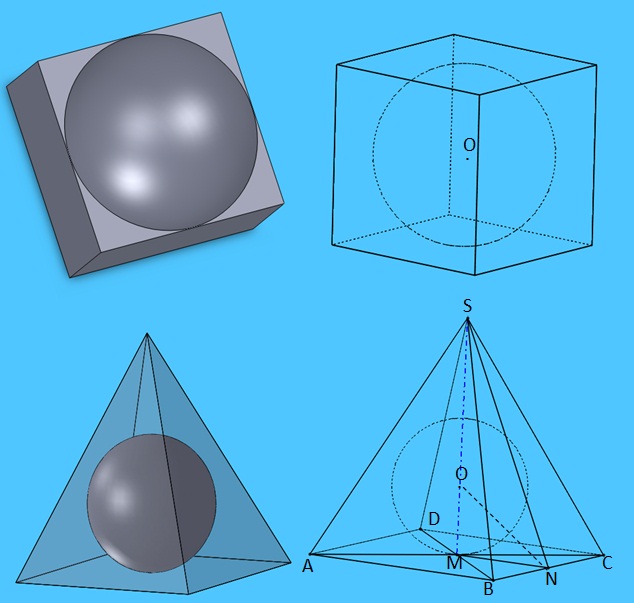
Комбінації
Циліндр, вписаний у кулюОснови циліндра є рівновіддаленими від центра кулі .Ця комбінація тіл є симетричною відносно будь-якої площини, що проходить через центр кулі паралельно твірним циліндра.Куля, вписана в конусПлощина, яка містить вісь конуса, є площиною симетрії . Осьовий переріз комбінації є рівнобедреним трикутником, у який вписане колоПризмою, вписаною в циліндр , називається така призма, в якої площинами основ є площини основ циліндра, а бічними ребрами — твірні циліндра. Отже, висоти призми й циліндра збігаються, а основи призми є вписаними многокутниками для основ циліндра.Пірамідою, описаною навколо конуса, називається піраміда, в основі якої лежить многокутник, описаний навколо основи конуса, а вершина збігається з вершиною конуса.

Призма
Призма (n-кутна) – це многогранник, у якого дві грані рівні n-кутники, які лежать у паралельних площинах, а інші n граней – паралелограми.Многокутники називаються основами призми, а паралелограми – бічними гранями. Сторони бічних граней та основ називаються ребрами призми. Кінці ребер називаються вершинами призми. Бічними ребрами називаються ребра, які не належать основам.
a
Тіло обертання
Тіла обертання — об'ємні тіла, що виникають при обертанні плоскої фігури, обмеженої кривою, навколо осі, що лежить в тій же площині.Циліндр — тіло, яке складається з двох кругів, які суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих кругів. Круги називаються основами циліндра, а відрізки, що сполучають відповідні точки кіл кругів, — твірними циліндра.
a
Піраміда
Піраміда (також рогівниця, гостриця, остриця) — багатогранник, який складається з плоского багатокутника і точки (яка не лежить у площині основи) та всіх відрізків, що сполучають вершину піраміди з точками основи. Відрізки, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами.Пряма піраміда це піраміда із вершиною, яка розміщена прямо над центром її основи. Не правильні піраміди називають похиленими пірамідами. Правильна піраміда має в основі правильний многокутник.
a