Великая теорема Ферма

Эллиптические кривые

Ютака Танияма(1927-1958)

На международном симпозиуме в Токио он выдвинул невообразимое доказательство, используя так называемое модулярные формы. Это фигуры,имеющие четыре измерения, которые мы с вами с нашими трехмерными мозгами едва ли можем представить себе. К тому же обладают они необыкновенной симметрией. Сдвигай их в любом направлении, поворачивай как угодно, меняй местами фрагменты, зеркально отражай и так далее, при этом вид их ничуть не измениться. Так вот,пытался доказать Танияма не саму теорему Ферма,а то, что модулярным функциям соответствуют кривые обычных эллипсов, которые можно разложить в нормальный числовой ряд. Однако коллеги его не поняли, и через три года гениальный японец, следуя самурайским традициям, поканчил с собой. Он был первым, кого проклятая загадка Ферма- да, будь она в этих случаях проклтая-довела до такого шага.

Уайлс Эндрю Джон(1953)

Первый вариант своего доказательства Уайлс опубликовал 1993 году ( после семи лет напряженной работы) , но вскоре обнаружился серьезный пробел; с помощью Ричарда Лоуренса Тейлора проьел удалось достаточно быстро ликвидировать. В 1995 году был опубликован завершающий вариант.

Ричард Тейлор(1962)

Геометрический подход

Луис Джоэл Морделл
(1888-1972)

$Луис Джоэл Морделл (1888-1972)$

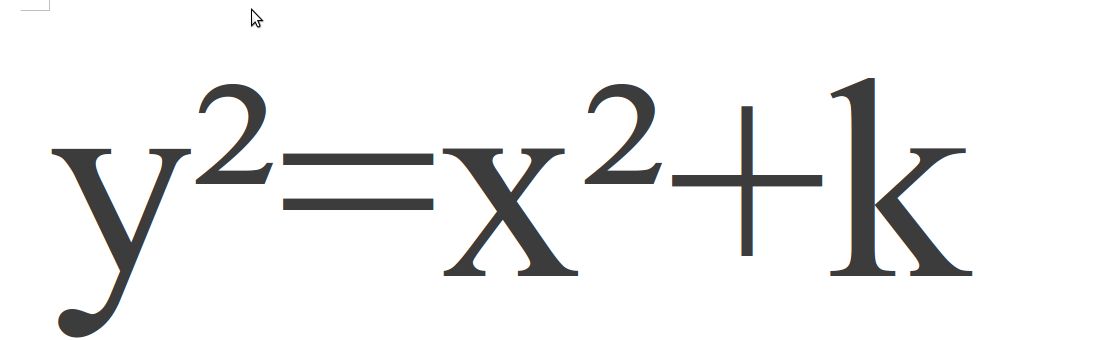
изучая это уравнение,в 1922 году, английский математик Луис Морделл выдвинул гипотезу, что число рациональных точек на алгебраической кривой степени выше, чем вторая.

Герд Фальтингс(28 июля 1954)

Фалтингсу удалось доказать, что, поскольку такие поверхности всегда имею несколько дыр, связанное с ними уравнение Ферма могло бы иметь лишь конечное множество решений в целых числах. Число решений могло быть любым-от нуля, как предполагал Ферма,до миллиона или миллиарда. Таким образом, Фалтингс не доказал Великую теорему Ферма, но по крайне мере сумел отвергнуть возможность существования y уравнения Ферма бесконечно многих решений.

Алгебраический подход

Леонард Эйлер
(1707-1783)

Занимаясь доказательством теоремы Ферма для n=3, Эйлер высказал предположение, что верно более общее утверждение: если сложить n-1 слагаемое, каждое из которых равной n-й степени натурального числа( при n>2), в результате не может получить n-я степень натурального числа.
Эта гипотеза оказалась неверна уже при n=4. Наиболее простой опровергающий пример к ней выглядит так:

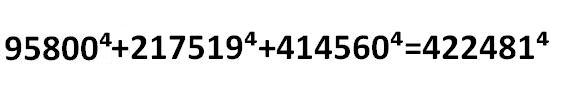
Пьер Ферма
(1601-1665)

Опубликовал доказательства частного случая для n=4

Куммер Эрнст Эдуард(1810-1893)

Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением т.н. иррегулярных простых 37, 59, 67.

Cофи Жермен
(1776-1831)

Занималась теорией чисел. Доказала так называемой "Первый случай" Великой теоремой Ферма для простых чисел Софи Жермен n, то есть таких простых чисел n, что 2n+1 тоже простое.

Ламе Габриель(1795-1810)

Доказал случай для n=7

$Ио́ганн Пе́тер Гу́став Лежён Дирихле́ (1805-1859)$

Ио́ганн Пе́тер Гу́став Лежён Дирихле́
(1805-1859)

В 1825 году Дирихле вместе с А. Лежандром доказал великую теорему Ферма для частного случая n=5.