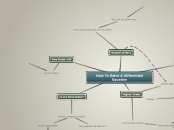
How To Solve A Differential Equation

Can You Integrate Directly?

Yes: Inegrate and solve for Y

No: Is it Seperable?

Seperable?

Yes: Integrate and solve for Y

No: Can you use the Integrating Factor Method?

Integrating Factor Method

What is the Integrating Factor?

Multiply by the Integrating Factor

Finally, Solve for Y

Use the Laplace

Solve for Y

Take the Inverse of the Laplace

Non-Homogeneous

First, Find the Homogenous Solution

Then Find the Particular Solution

Undetermined Coefficeint Method

Variation of Parameters Method

Subtopic

Homogeneous?

Form The Characteristic Equation

Using the C.E's, Find its roots

Real Roots

Solution: y(t)=c1e^(r1t)+c2e^(r2t)

Repeated Roots

Solution: y(t)=c1e^(r1t)+c2te^(r1t)

Complex Imaginary Roots

Solution: y(t)=e^(At)(c1cosBt+c2sinBt)

Form the Characteristic Eq of the Matrix

Solve for the Eigenvalues

Plug in those Eigenvalues

Obatin Eigenvectors

Form the General Solution

System Method

Second Order Method

High Order Method

Homogeneous

Non-Homogeneous