Integrales definidas
¿Qué es?
La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b], se llama integral definida de la función entre los puntos a y b al área de la porción del plano que está limitada por la función, el eje horizontal OX y las rectas verticales de ecuaciones x = a y x = b.
La Integral como Límite del Área
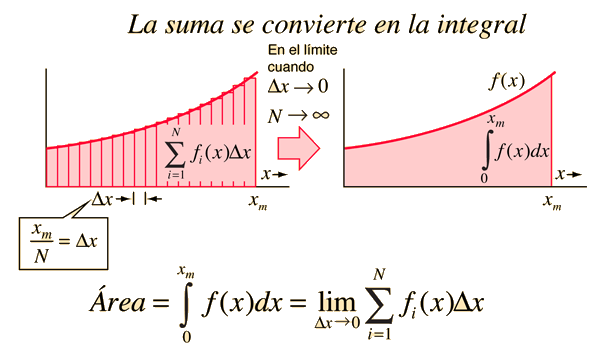
La aproximación al valor del área bajo una curva puede mejorarse tomando rectángulos de aproximación mas estrechos. La idea de la integral es incrementar el número de rectángulos N hacia el infinito, tomando el límite cuando el ancho del rectángulo tiende a cero.
Motivation
Aunque el concepto de área geométrica es una forma conveniente de visualizar una integral, la idea de la integración es mucho mas general. Cualquier variable física continua puede ser "troceada" en incrementos infinitesimales (elementos diferenciales) de modo que, la suma del producto de ese "ancho" por el valor de la función se acerca a una suma infinita. La integral es una herramienta poderosa para modelar problemas físicos que impliquen cantidades que varien continuamente.
Ejemplos de Integral de Área
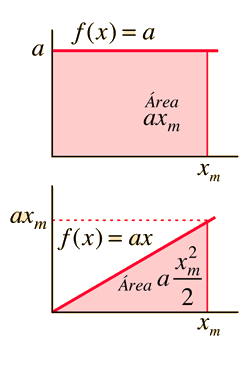
Los ejemplos de área de geometrías simples, pueden reforzar la idea de la integral como el área bajo una curva. Para una función que es una constante a, el área formada por la función es exactamente un rectángulo.
Motivation
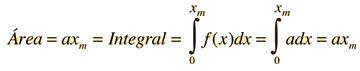
Aquí la conclusión general es que la integral de una constante es exactamente la constante multiplicada por la variable de integración x.
En una función f(x) = ax, el área es un triángulo


La progresión nos lleva a la forma general de la integral como un polinomio de x:
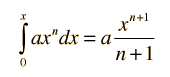
Aproximaciones a la Integral de Área
El área bajo cualquier curva continua se puede obtener aproximadamente, dibujando un número de rectángulos. La integral es el límite para un número infinito de rectángulos.
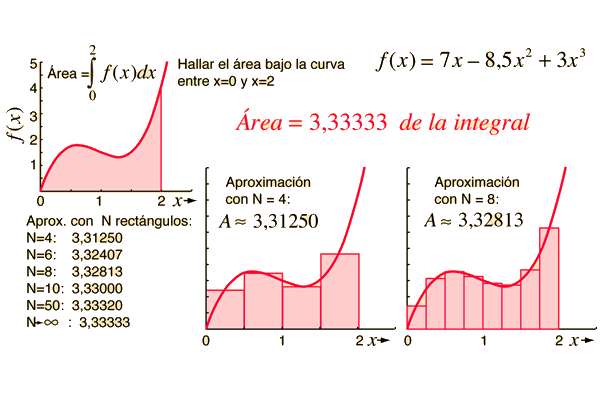
Obstacles
Ejemplos de Integral de Área
Las integrales son útiles para el cálculo del área bajo curvas, que se pueden obtener de forma aproximada, por medio de métodos geométricos.
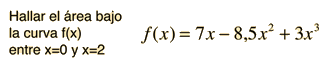
Esta es una integral de tipo polinómico que se calcula sumando las partes integrantes.

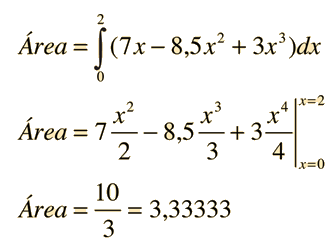
Área bajo una curva
¿Qué es?
Nosotros conocemos muchas fórmulas para calcular el área de diferentes figuras geométricas. Por ejemplo, para calcular el área A de un triángulo con base b y altura h, usamos la fórmula:

Sin embargo, no sabemos cómo calcular el área que hay entre la parábola y = x^2, el eje x y las rectas verticales x = 0 y x = 1.

Sin embargo, podemos aproximar el valor de esta área si vamos seccionando el intervalo (0,1) y dibujamos rectángulos con altura igual a la ordenada y_i = x_i^2. Para esto tenemos dos opciones, bien dibujamos los rectángulos de manera que una parte del mismo quede por encima de la parábola, bien los dibujamos de manera que una parte quede por debajo de la parábola.
La aproximación que hagamos tendrá, en el primer caso un error por exceso, es decir, será mayor al valor del área que buscamos. En el segundo caso el área aproximada será un poco menor al área debajo de la parábola.

Podemos calcular el área de cada rectángulo que queda por encima de la parábola y de los que quedan por debajo y ordenar esta información en una tabla:

El tamaño del error dependerá de la cantidad de rectángulos que dibujemos para hacer la aproximación. A mayor cantidad de rectángulos, las regiones de cada rectángulo que queden por encima o por debajo serán cada vez más pequeños que la suma de todos esos errores será despreciable:

En la siguiente tabla se muestran los resultados obtenidos para diferente número de rectángulos en el intervalo (0,1):

de la tabla se hace evidente que el área tiende a un número A que satisface:

Si dibujamos más rectángulos obtendremos una mejor aproximación. Entonces, si encontramos el límite de la suma de las áreas de todos los rectángulos que dibujamos bajo la curva cuando el número de rectángulos tiende a infinito, debemos obtener el área bajo la curva y = f(x) desde desde x = a hasta x = b. Es decir,

representa el área que buscamos. Observa que la base del rectángulo mide \D x = (b - a) / n porque hemos decidido hacer n particiones del mismo tamaño todas y que la altura del rectángulo puede ser calculada utilizando la función: f(x_i)

Cuando el número de particiones (n) crece, el error que se comete al aproximar el área bajo la curva con el área del rectángulo, cada vez es más pequeño y cuando n tiende a infinito, \D x tiende a cero. Debido a esto decimos que el área bajo la curva es:

Ejemplo
alcula el área bajo la parábola y = x^2 en el intervalo (0,1) usando el límite:

Subtopic
Por definición:

Primero haremos la suma y después vamos a calcular el límite cuando n tiende a infinito.

Pero ya habíamos mencionado que:

Entonces, podemos sustituir esto y obtener:

Entonces, el área bajo la parábola y=x^2 desde x = 0 hasta x = 1 es 1/3 exactamente.
Este mismo procedimiento es el que realmente hacemos cuando calculamos la integral definida, pues esta es la forma como se define.