La funzione
Definizione
Tipologie
Algebrica
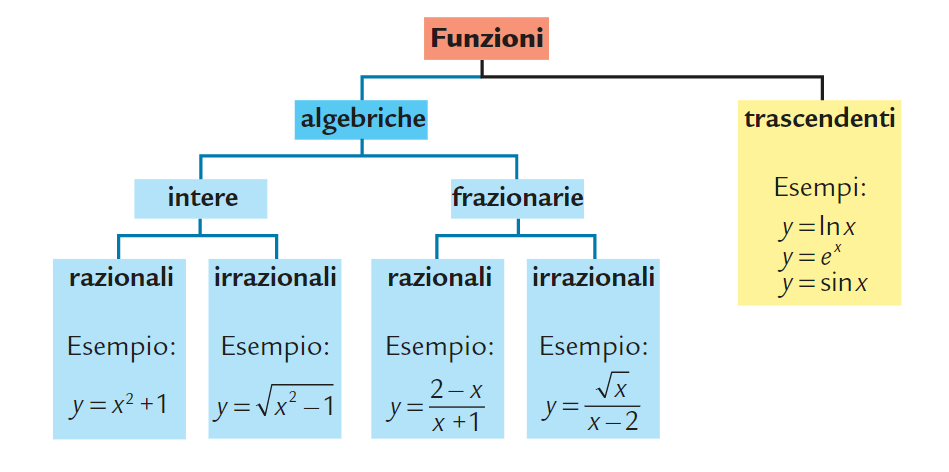
Nella quale compaiono solo operazioni di tipo algebrico: addizione sottrazione, moltiplicazione, divisione, potenza.
Essa può dividersi in:
RAZIONALE e IRRAZIONALI
che si dividono a loro volta in fratte e intere.
Trascendente
La quale contiene operazioni trascendenti: logaritmo, esponenziale o le funzioni goniometriche.
Si articolano in LOGARITMICHE, GONIOMETRICHE ed ESPONENZIALI.
Studio

Dominio
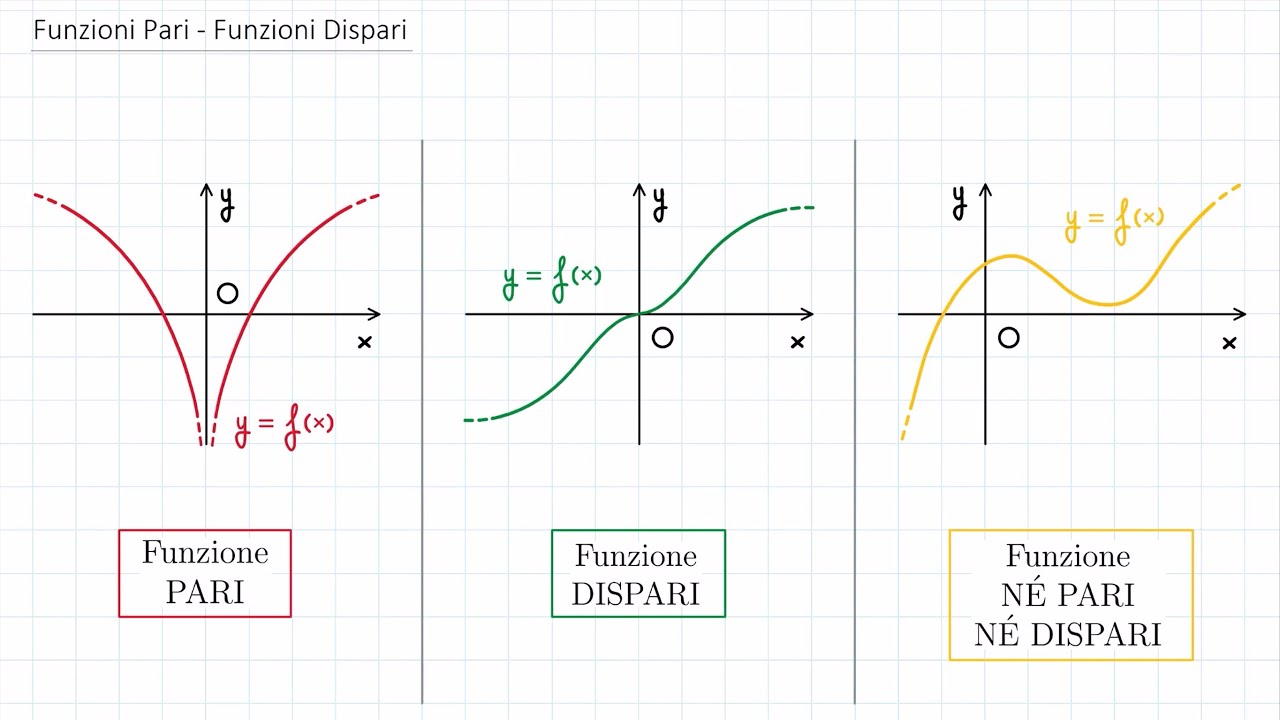
Simmetrie pari/dispari
Asintoti
verticale
orizzontale
obliquo
Calcolo derivata prima e ricerca punti stazionari
Casi particolari di funzioni non derivabili in punti appartenenti al dominio
Natura punti stazionari
Max, min, flessi a tangente orizzontale
Calcolo derivata seconda e ricerca dei punti di flesso
Studio concavità
Grafico
Esempi di funzione matematica

Sottoargomento
Esempi di funzione non matematica
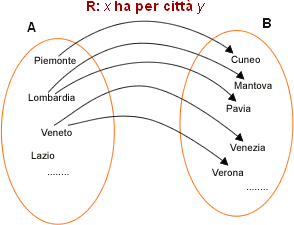
Sottoargomento
Link utili
Video
Sottoargomento