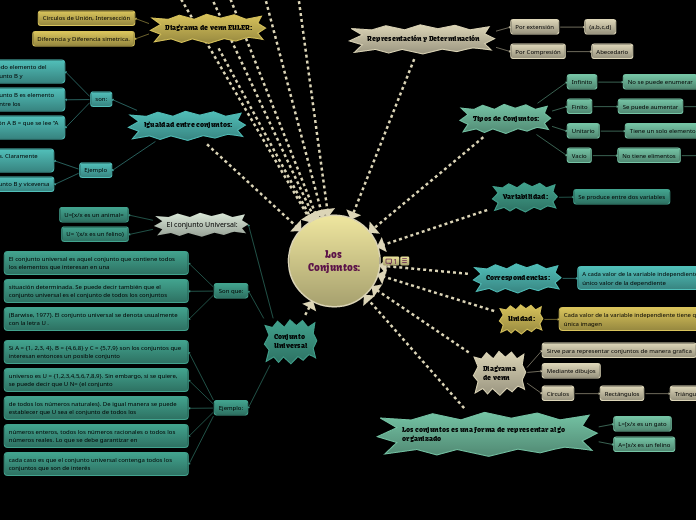
Los Conjuntos:
Representación y Determinación
Por extensión
(a,b,c,d)
Por Compresión
Abecedario
Tipos de Conjuntos:
Infinito
No se puede enumerar
P= 0,1,2,3...etc.
Finito
Se puede aumentar
L= 2,4,6,8...etc.
Unitario
Tiene un solo elemento
A= ( 7 )
Vacio
No tiene elimentos
u= ( )
Variabilidad:
Se produce entre dos variables
Correspondencias:
A cada valor de la variable independiente le corresponde un único valor de la dependiente
Unidad:
Cada valor de la variable independiente tiene que tener una única imagen
Diagrama de venn
Sirve para representar conjuntos de manera grafica
Mediante dibujos
Círculos
Rectángulos
Triángulos
Los conjuntos es una forma de representar algo organizado
L=[x/x es un gato
A=[x/x es un felino
¿Qué tanto sabemos realmente acerca de los conjuntos?
¿ Que son y como se representan?
Objetos
Se representan
Grupos de conjuntos
Pueden ser numéricos
Personas u animales
Las caracteristicas de un Conjunto, son aquellos grupos de objetos,numeros o personas que se representan por medio de agrupaciones.
Winsniewski dice:
El conjunto A arbitrario y X es un elemento que forma parte de dicho conjunto.
XeA= X PERTENECE AL CONJUNTO A
No pertenece E
. Para denotar que x no es un elemento del conjunto A,
se escribe x A
Representación:
Los numero naturales son multiplos de 2
A = {2, 4,6,8,10,...}
Conjunto A por extensión
A = {Todos los números que son múltiplos de 2}
Diferencia entre conjuntos
Diferencia
A B xx A x B − = ∈ ∧∉ { : }
Relacionada a la diferencia
se lee “A menos B es el conjunto de todos los elementos x tales que x pertenece al conjunto A y x no
pertenece al conjunto B”.
Diagrama de venn EULER:
Círculos de Unión, Intersección
Diferencia y Diferencia simetrica.
Igualdad entre conjuntos:
son:
Dos conjuntos A y B se dicen iguales si todo elemento del conjunto A es a su vez elemento del conjunto B y
al mismo tiempo todo elemento del conjunto B es elemento del conjunto A. La relación de igualdad entre los
conjuntos A y B se denota con la expresión A B = que se lee “A es igual a B” (Mejía et al., 2005).
Ejemplo
A = {1,2,3} y B = {3, 2,1} son conjuntos iguales. Claramente todo elemento del conjunto A es a su vez
elemento del conjunto B y viceversa
Conjunto Universal
El conjunto Universal:
U=[x/x es un animal=
U= ´(x/x es un felino)
Son que:
El conjunto universal es aquel conjunto que contiene todos los elementos que interesan en una
situación determinada. Se puede decir también que el conjunto universal es el conjunto de todos los conjuntos
(Barwise, 1977). El conjunto universal se denota usualmente con la letra U .
Ejemplo:
Si A = {1, 2,3, 4}, B = {4,6,8} y C = {5,7,9} son los conjuntos que interesan entonces un posible conjunto
universo es U = {1,2,3,4,5,6,7,8,9}. Sin embargo, si se quiere, se puede decir que U N= (el conjunto
de todos los números naturales). De igual manera se puede establecer que U sea el conjunto de todos los
números enteros, todos los números racionales o todos los números reales. Lo que se debe garantizar en
cada caso es que el conjunto universal contenga todos los conjuntos que son de interés