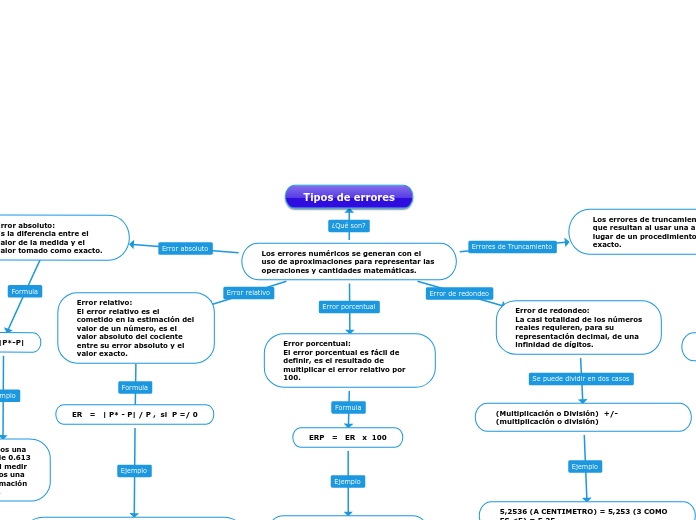
Los errores numéricos se generan con el uso de aproximaciones para representar las operaciones y cantidades matemáticas.
Error absoluto:
Es la diferencia entre el valor de la medida y el valor tomado como exacto.
EA=|P*-P|
Tenemos una recta de 0.613 cm y al medir tenemos una aproximación de 0.6.
Error relativo:
El error relativo es el cometido en la estimación del valor de un número, es el valor absoluto del cociente entre su error absoluto y el valor exacto.
ER = | P* - P| / P , si P =/ 0
Una piscina con capacidad de 719 m3, tiene un error absoluto menor a medio metro cúbico, (error < 0,5 m3). Entonces el error relativo (0,5/719) es de 6,954 .
Error porcentual:
El error porcentual es fácil de definir, es el resultado de multiplicar el error relativo por 100.
ERP = ER x 100
El resultado del error relativo es 6,954. Entonces, el error porcentual es 0,0695.
Los errores de truncamiento son aquellos que resultan al usar una aproximación en lugar de un procedimiento matemático exacto.
Se utiliza la serie infinita de Taylor.
Rn= ((ƒ(n+1) (ξ))/(n+1)!)hn+1
Dado el número real 3,1415926, consideramos los 4 dígitos a la derecha de la coma decimal. El resultado es:
3,1415
Tipos de errores
Error de redondeo:
La casi totalidad de los números reales requieren, para su representación decimal, de una infinidad de dígitos.
(Multiplicación o División) +/- (multiplicación o división)
5,2536 (A CENTIMETRO) = 5,253 (3 COMO ES <5) = 5,25.